Proposed:
$$\int_{0}^{1}\cos(\ln x)\cdot{\mathrm dx\over 1+x^2}={\pi\over 4}\cdot{1\over \cosh\left({\pi\over 2}\right)}\tag1$$
My try:
$x=\tan u\implies dx=\sec^2 u du$, then $(1)$ becomes
$$\int_{0}^{\pi/4}\cos(\ln\tan u)\mathrm du\tag2$$
Recall of $$\int_{0}^{\pi/2}\ln\sin x\mathrm dx=\int_{0}^{\pi/2}\ln\cos x\mathrm dx=-{\pi\over 2}\ln(2)\tag3$$
First note that
$$2 \int^1_0 \frac{\cos(\log x) }{x^2+1}\,dx = \int^\infty_0 \frac{\cos(\log x)}{x^2+1}\,dx$$
Integrate the following function
$$f(z) = \frac{e^{i\log(z)}}{z^2+1}$$
Around a semi-circle in the upper half place. Where we avoid the branch point at $z=0$ by a semi-circle. We assume that the branch cut is taken on the negative imaginary axis.
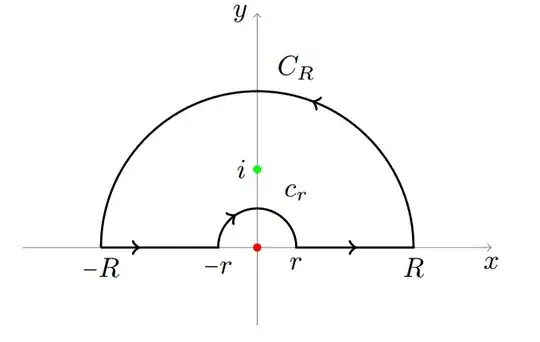
$$\int^{-r}_{-R}f(z) \,dz +\int^{R}_{r}f(z) \,dz+ \int_{C_R}f(z)\,dz+\int_{c_r}f(z)\,dz =2\pi i \mathrm{Res}(f,i)$$
The integral on semi-circles
\begin{align}\left|\int_{C_R} \frac{e^{i\log(z)}}{z^2+1}\right| &\leq R \int^{\pi}_0 \left|\frac{e^{i \log(R e^{it})}}{R^2e^{2it}+1}\right| dt\\ &\leq R \int^{\pi}_0 \frac{e^{i \log R-t}}{|R^2-1|} dt\\ &\leq \frac{R}{R^2-1} \int^{\pi}_0 e^{-t} dt\\ &\leq \frac{R(1-e^{-\pi})}{R^2-1} dt \sim_{\infty} 0 \end{align}
Similarily
$$\lim_{r \to 0}\int_{C_r} \frac{e^{i\log(z)}}{z^2+1} = 0$$
Hence we have as $ R \to \infty , r \to 0 $ $$\int_{-\infty}^0 \frac{e^{i\log|x|-\pi}}{x^2+1}\,dx +\int^\infty_0 \frac{e^{i\log(x)}}{x^2+1}\,dx =2\pi i \mathrm{Res}(f,i)$$
$$(1+e^{-\pi})\int^\infty_0 \frac{e^{i\log(x)}}{x^2+1}\,dx =2\pi i \mathrm{Res}(f,i)$$
Note that
$$\mathrm{Res}(f,i) = \frac{e^{i\log(i)}}{2i} = \frac{e^{-\pi/2}}{2i}$$
Hence
$$\int^\infty_0 \frac{e^{i\log(x)}}{x^2+1}\,dx =\pi \frac{e^{-\pi/2}}{1+e^{-\pi}} = \frac{\pi}{e^{\pi/2}+e^{-\pi/2}} = \frac{\pi}{2}\mathrm{sech}\left( \frac{\pi}{2}\right)$$
Which implies that
$$\int^\infty_0 \frac{\cos(\log x)}{x^2+1}\,dx = \frac{\pi}{2}\mathrm{sech}\left( \frac{\pi}{2}\right)$$
Hence we have our result
$$\int^1_0 \frac{\cos(\log x)}{x^2+1}\,dx = \frac{\pi}{4}\mathrm{sech}\left( \frac{\pi}{2}\right)$$
The Tikz code for the contour drawing
\begin{tikzpicture}[decoration={markings,
mark=at position 0.5cm with {\arrow[line width=1pt]{>}},
mark=at position 2cm with {\arrow[line width=1pt]{>}},
mark=at position 3.85cm with {\arrow[line width=1pt]{>}},
mark=at position 7cm with {\arrow[line width=1pt]{>}}
}
]
% The axes
\draw[help lines,->] (-3,0) -- (3,0) coordinate (xaxis);
\draw[help lines,->] (0,-1) -- (0,3) coordinate (yaxis);
% The path
\path[draw,line width=0.8pt,postaction=decorate] (-2,0) node[below] {$\minus
R$} -- (-0.5,0) node[below] {$\minus r$} -- (-0.5,0) arc (180:0:0.5) --
(0.5,0) node[below] {$r$} -- (2,0) node[below] {$R$} arc (0:180:2);
% The labels
\node[below] at (xaxis) {$x$};
\node[left] at (yaxis) {$y$};
\node at (0.5,0.7) {$c_{r}$};
\node at (0.5,2.3) {$C_{R}$};
\node at (-0.2,1) {$i$};
\draw[red,fill=red] (0,0) circle (.3ex);
\draw[green,fill=green] (0,1) circle (.3ex);
\end{tikzpicture}
Combining the substituion $\ln x =-t$, the fact that $\cos t$ is an even function and $\sin t$ an odd one we get \begin{equation*} I = \int_{0}^{1}\cos(\ln x)\dfrac{1}{1+x^2}\, dx = \int_{0}^{\infty}\cos t\dfrac{e^{-t}}{1+e^{-2t}}\, dt = \dfrac{1}{4}\int_{-\infty}^{\infty} e^{-i\omega t}\dfrac{1}{\cosh t}\, dt. \end{equation*} But it well known that the Fourier transform of $\dfrac{1}{\cosh t}$ is $\dfrac{\pi}{\cosh\left(\frac{\pi \omega}{2}\right)}$, where the Fourier transform is given by \begin{equation*} \hat{f}(\omega) = \int_{-\infty}^{\infty}e^{-i\omega t}f(t)\, dt. \end{equation*} Consequently \begin{equation*} I = \dfrac{\pi}{4\cosh\left(\frac{\pi}{2}\right)}. \end{equation*}
Another approach, Note that
$$2 \int^1_0 \frac{\cos(\log x) }{x^2+1}\,dx = \int^\infty_0 \frac{\cos(\log x)}{x^2+1}\,dx$$
Now we use that
$$x^i= e^{i\log(x)} = \cos(\log x)+i \sin(\log x)$$
Consider the integral
$$\int^\infty_0 \frac{x^i}{x^2+1}\,dx$$
Let $x^2 = y $
$$\frac{1}{2}\int^\infty_0 \frac{y^{(i-1)/2}}{y+1}\,dy$$
Note that
$$\int^\infty_0 \frac{t^{x-1}}{(t+1)^{x+y}}\,dt = B(x,y)$$
We conclude that
$$\frac{1}{2}\int^\infty_0 \frac{y^{(i-1)/2}}{y+1}\,dy= \Gamma\left( \frac{i+1}{2}\right)\Gamma\left(1-\frac{i+1}{2} \right) = \pi \csc\left(\frac{i+1}{2}\pi \right) = \frac{\pi}{2}\mathrm{sech}\left(\frac{\pi}{2} \right)$$
Hence
$$ \int^1_0 \frac{\cos(\log x) }{x^2+1}\,dx = \frac{1}{2} \Re \int^\infty_0 \frac{x^i}{x^2+1}\,dx =\frac{\pi}{4}\mathrm{sech}\left(\frac{\pi}{2} \right) $$
$\newcommand{\bbx}[1]{\,\bbox[8px,border:1px groove navy]{\displaystyle{#1}}\,} \newcommand{\braces}[1]{\left\lbrace\,{#1}\,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\,{#1}\,\right\rbrack} \newcommand{\dd}{\mathrm{d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,\mathrm{e}^{#1}\,} \newcommand{\ic}{\mathrm{i}} \newcommand{\mc}[1]{\mathcal{#1}} \newcommand{\mrm}[1]{\mathrm{#1}} \newcommand{\pars}[1]{\left(\,{#1}\,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\root}[2][]{\,\sqrt[#1]{\,{#2}\,}\,} \newcommand{\totald}[3][]{\frac{\mathrm{d}^{#1} #2}{\mathrm{d} #3^{#1}}} \newcommand{\verts}[1]{\left\vert\,{#1}\,\right\vert}$ \begin{align} \int_{0}^{1}\cos\pars{\ln\pars{x}}\,{\dd x \over 1 + x^{2}} & = \Re\int_{0}^{1}\expo{\ic\ln\pars{x}}\,{\dd x \over 1 + x^{2}} = \Re\int_{0}^{1}{x^{\ic} \over 1 + x^{2}}\,\dd x = \Re\int_{0}^{1}{x^{\ic} - x^{\ic + 2} \over 1 - x^{4}}\,\dd x \\[5mm] & = {1 \over 4}\,\Re\int_{0}^{1}{x^{\ic/4 -3/4} - x^{\ic/4 - 1/4} \over 1 - x}\,\dd x \\[5mm] & = {1 \over 4}\,\Re\pars{% \int_{0}^{1}{1 - x^{\ic/4 - 1/4} \over 1 - x}\,\dd x - \int_{0}^{1}{1 - x^{\ic/4 - 3/4} \over 1 - x}\,\dd x} \\[5mm] & = {1 \over 4}\,\Re\pars{H_{\ic/4 - 1/4} - H_{\ic/4 - 3/4}}\qquad \pars{~H_{z}:\ Harmonic\ Number~} \\[5mm] & = {1 \over 4}\ \overbrace{\Re\pars{H_{\ic/4 - 1/4} - H_{-\ic/4 - 1/4}}}^{\ds{=\ 0}}\ -\ {1 \over 4}\ \underbrace{\Re\pars{\pi\cot\pars{\pi\bracks{{3 \over 4} - {\ic \over 4}}}}} _{\ds{\substack{\ds{=\ -\,{\pi \over \cosh\pars{\pi/2}}\\ {\tiny after\ a\ tedious\ algebraic\ task}}}}} \\[5mm] & = \bbx{{1 \over 4}\,\pi\,\mrm{sech}\pars{\pi \over 2}} \end{align}
Let $$ f(z)=\frac{2z+1}{(2z+1)^2+1} $$ and hence $f(z)$ has two poles $z_{1,2}=-\frac12\pm\frac12 i$. Using $t=-\ln x$, then one has \begin{eqnarray} &&\int_{0}^{1}\cos(\ln x)\cdot{\mathrm dx\over 1+x^2}\\ &=&\int_{0}^{\infty}\cos(t)\cdot{e^{-t}\mathrm dt\over 1+e^{-2t}}\\ &=&\int_{0}^{\infty}\sum_{n=0}^\infty (-1)^ne^{-(2n+1)t}\cos(t)\mathrm dt\\ &=&\sum_{n=0}^\infty (-1)^n\frac{2n+1}{(2n+1)^2+1}\\ &=&\frac12\sum_{n=-\infty}^\infty (-1)^n\frac{2n+1}{(2n+1)^2+1}\\ &=&-\frac12\bigg[\text{Res}(f(z)\csc(\pi z),z_1)+\text{Res}(f(z)\csc(\pi z),z_2)\bigg]\\ &=&{\pi\over 4}\cdot{1\over \cosh\left({\pi\over 2}\right)}. \end{eqnarray} Here $$ \sum_{n=-\infty}^{\infty}(-1)^nf(n)=-\sum_{k=1}^n \text{Res}(f(z)\csc(\pi z),a_k) $$ where $a_1,a_2,\cdots, a_n$ are poles of $f$.
