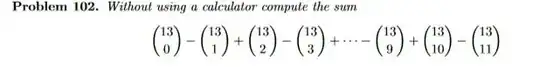0

In general I want to know how to solve these types of questions. I know that you have to use the binomial theorem.

Exmple

or $\binom{99}{1}-\binom{99}{2}+\binom{99}{3}-\binom{99}{4}+...+-\binom{99}{96}+\binom{99}{97}-\binom{99}{98}$

Please don't just give me the answers I want to understand what you are doing.

Phillip Mc
  • 159

3 Answers3

0

Notice that from a class of $n$ people, the number of ways to choose $i$ people to be in a team is equal to the number of ways to choose $n-i$ people to be not in the team. That is, we have:

$$\binom{n}{i} = \binom{n}{n-i}$$

Hence by pairing the $i$-th and $(n-i)$-th term, they get cancelled out.

$$\sum_{i=0}^{11} \binom{13}{i}=\binom{13}{0}-\binom{13}{1}$$

Similarly for the second question.

Pair $\binom{99}{1}$ with $\binom{99}{98}$. Pair $\binom{99}{2}$ with $\binom{99}{97}$ and etc.

Siong Thye Goh
  • 149,520
  • 20
  • 88
  • 149
0

Hint: $${{n} \choose {k} }={{n} \choose {n-k} }$$

For instance ${{13}\choose {2} }-{{13} \choose {11} }=0$

The most of the sum is $0$.

callculus42
  • 30,550
  • Does this apply to only this instance? what about the second one?. – Phillip Mc May 07 '17 at 19:00
  • And why is it $\binom{n}{n-k}$ – Phillip Mc May 07 '17 at 19:05
  • No the second one is similar. $${{99} \choose {1} }={{99} \choose {98} }$$. Now you compare the second summand and the second to last summand. You go on like this. You will end up with ${{99} \choose {49} }-{{99} \choose {50} }$. This are the two summand in the middle of term. – callculus42 May 07 '17 at 19:09
  • ${n\choose k}=\frac{n!}{(n-k)!\cdot k!}$ For the binomial coefficient the lower number can be $k$ or $n-k$. The value of the binomial coefficient is equal in both cases. – callculus42 May 07 '17 at 19:15
0

Expand binomial theorem for $(1+x)^{13}$:

$$(1+x)^{13}=\binom{13}{0}x^{0}+\binom{13}{1}x^{1}+ \ldots +\binom{13}{12}x^{12}+\binom{13}{13}x^{13}$$

Now put $x=-1$ to get :

$$\binom{13}{0}-\binom{13}{1}+\binom{13}{2} \ldots +\binom{13}{12}-\binom{13}{13}=(1-1)^{13}=0$$

Hence required sum :

$$\binom{13}{0}-\binom{13}{1}+\binom{13}{2} \ldots -\binom{13}{11} =\binom{13}{13}-\binom{13}{12}$$

Jaideep Khare
  • 19,293