Mistake with using residue theory for calculating $\int_{-\infty}^{\infty}\frac{\sin(x)}{x}dx$

Question

In physics, we do contour integrals in a not so rigorous way most of the times. Now, I want to use a trick to compute $$\int_{-\infty}^{\infty}\frac{\sin(x)}{x}dx$$ using residue theory. I find:
$$\int_{-\infty}^{\infty}\frac{\sin(x)}{x}dx=2\pi$$which is clearly wrong since the correct value is $\pi$.

I don't know what I am doing wrong here but I think it might have to do with using the residue theorem in a clumsy way. Any help in finding the mistake will be much appreciated.

My solutions is the following(sorry if my notation(arguments) is too awkward(or not rigorous enough)):
$$\int_{-\infty}^{\infty}\frac{\sin(x)}{x}dx=Im\left[\int_{-\infty}^{\infty}\frac{e^{ix}}{x}dx\right]=Im\left[\lim_{ε\to0}\int_{-\infty}^{\infty}\frac{e^{ix}}{x-iε}dx\right]$$ which has a residue just above $x=0$ on the complex plane.
Now, consider the following integration paths:

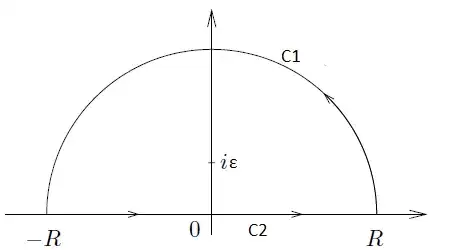
So, I can write the above integral as:
$$Im\left[\lim_{ε\to0}\int_{-\infty}^{\infty}\frac{e^{ix}}{x-iε}dx\right]=Im\left[\lim_{ε\to0}\int_{C2}\frac{e^{ix}}{x-iε}dx\right]$$(of course $R\to \infty$)
Now, if we integrated the same integrand but the path was $C1$, it would give zero since the integrand tends to zero for large $Im[x]$ on the upper plane(this argument was used by a professor of our for a scattering problem in quantum mechanics).
So, we can now write:
$$Im\left[\lim_{ε\to0}\int_{C2}\frac{e^{ix}}{x-iε}dx\right]=Im\left[\lim_{ε\to0}\int_{C1+C2}\frac{e^{ix}}{x-iε}dx\right]$$which is an integral along a closed path that encloses the pole(residue) at $x=iε$. So, I can use the residue theorem to find that the integral is equal to: $$Im[\lim_{ε\to0}2\pi i Res(e^{i(iε)})]=2\pi $$ which is clearly off by a factor of 2.
So, which of the above arguments is wrong?

Answer 1

The problem here is actually quite subtle, you've used the residue theorem correctly to evaluate the entire contour integral, and you've correctly identified that the integral over $C_1$ goes to $0$ as $R \to \infty$. This gave you a correct value for the imaginary part of the integral (for $\epsilon > 0$) $$\operatorname{Im}\left(\int_{-\infty}^{\infty}\frac{e^{iz}}{z - i \epsilon}d z\right) = 2\pi e^{-\epsilon}$$ which you can confirm here.

But, the problem happens when taking the limit as $\epsilon \to 0$, in that there's no guarantee that

$$\lim_{\epsilon \to 0} \int_{-\infty}^{\infty}\frac{e^{iz}}{z - i \epsilon}d z = \int_{-\infty}^{\infty} \lim_{\epsilon \to 0} \frac{e^{iz}}{z - i \epsilon}d z$$ This is where the solution breaks down, and your discrepancy here is a nice demonstration of how swapping the order of the limits needs more justification - in particular remember that the integral is defined as a limiting process, so some fairly strong continuity arguments would be required to show the left and right above would be equal. Of course in physics, you're used to assuming everything is as continuous as you'd like! In this particular case, it turns out $\int_{-\infty}^{\infty}\frac{e^{iz}}{z - i \epsilon}d z$ isn't continuous at $\epsilon=0$, so here's where your mistake is.

Answer 2

The problem is that in this case,

$$\int_{-\infty}^\infty\lim_{\varepsilon\rightarrow0}\frac{\sin x}{x-i\varepsilon}dx\ne\lim_{\varepsilon\rightarrow0}\int_{-\infty}^\infty\frac{\sin x}{x-i\varepsilon}dx.$$

The left-hand side is what you want, but the right-hand side is what you actually calculated. Really, what you found was the limit as $\varepsilon\rightarrow0^+$. If you had instead had $\varepsilon$ approach $0$ from below, you would have gotten $0$ as your answer. The limit on the left-hand side works out the same whether $\varepsilon$ approaches $0$ from the right or the left, so the fact that we get two different answers for the right-hand side immediately tells us something is wrong.

While this isn't rigorous, you'll note that the correct answer is halfway between the $2\pi$ you found for $\varepsilon\rightarrow0^+$ and the $0$ you get for $\varepsilon\rightarrow0^-$.

Answer 3

You can't replace $\sin(x)$ by $\text{Im}\exp(ix)$ without taking the principal part of the integral. Now, if the goal is to find a different derivation of the integral that avoids that step, then one can proceed as follows. We'll then stick with $\sin(x)$ for a bit longer. Because $\frac{\sin(z)}{z}$ is free of singularities, we can move the integration contour down by $i\epsilon$ without problems, by Cauchy's theorem it will have the same value. In general,

$$\int_{-\infty}^{\infty}\frac{\sin(x)}{x}dx = \int_{C(\epsilon)}\frac{\sin(z)}{z}dz$$

where $C(\epsilon)$ is some arbitrary detour from minus to plus infinity and $\epsilon$ is a measure of the size of this detour. No limit of $\epsilon\to 0$ needs to be considered here. We then choose a detour that avoids the point $z = 0$ in some arbitrary way. Because we're then moving off the real axis with $\sin(z)$, we cannot replace $\sin(z)$ by $\text{Im}\exp(i z)$ in this approach, but we can write the integral as:

$$ \int_{C(\epsilon)}\frac{\sin(z)}{z}dz = \frac{1}{2 i}\int_{C(\epsilon)}\frac{\exp(iz) - \exp(-i z)}{z}dz = \frac{I^{+} - I^{-}}{2 i}$$

where

$$I^{\pm} = \int_{C(\epsilon)} \frac{\exp(\pm iz)}{z}dz$$

We can then compute the $I^{\pm}$ by closing the contour for $I^{+}$ in the upper half plane while closing it in the lower half plane for $I^{-}$. The residue theorem then yields that if $C(\epsilon)$ passes below the pole at $z = 0$, then $I^{+} = 2\pi i$ while $I^{-} = 0$, while if $C(\epsilon)$ passes above the pole at $z = 0$, then $I^{+} = 0$ and $I^{-} = -2\pi i$, therefore we always have that $I^{+} - I^{-} = 2\pi i$ and we find that:

$$\int_{-\infty}^{\infty}\frac{\sin(x)}{x}dx =\pi$$

Answer 4

If you are going to move the contour, you have to make sure that there are no singularities on the contour. The original integrand, $\frac{\sin(x)}x$, has no (non-removable) singularities, so we could move the contour: $$ \begin{align} &\int_{-R}^R\frac{\sin(x)}x\,\mathrm{d}x -\int_{-R-i\epsilon}^{R-i\epsilon}\frac{\sin(x)}x\,\mathrm{d}x \color{#C00}{+\int_R^{R-i\epsilon}\frac{\sin(x)}x\,\mathrm{d}x -\int_{-R}^{-R-i\epsilon}\frac{\sin(x)}x\,\mathrm{d}x}\\ &=\int_{\gamma_R}\frac{\sin(x)}x\,\mathrm{d}x\\[6pt] &=0 \end{align} $$ where the two red integral vanish as $R\to\infty$ since the integrands are less than $\frac1R$ and are over contours of bounded length ($\epsilon$). The integral over $\gamma_R$ is $0$ for all $R$ since there are no singularities inside the rectangular contour (indeed, in all of $\mathbb{C}$). Thus, $$ \int_{-\infty}^\infty\frac{\sin(x)}x\,\mathrm{d}x =\int_{-\infty-i\epsilon}^{\infty-i\epsilon}\frac{\sin(x)}x\,\mathrm{d}x $$ Now, the way I usually break this up is integrating $\frac{e^{ix}}{2ix}$ over a closed semi-circular contour in the upper half-plane ($\gamma_+$) and $-\frac{e^{-ix}}{2ix}$ over a closed semi-circular contour in the lower half-plane ($\gamma_-$), where the line of closure is $[-R-i\epsilon,R-i\epsilon]$. $\gamma_-$ does not contain any singularities of $-\frac{e^{-ix}}{2ix}$, and $\gamma_+$ contains the singularity of $\frac{e^{ix}}{2ix}$ at $x=0$.

That is, the integral is $2\pi i$ times the residue of $\frac{e^{ix}}{2ix}$ at $x=0$, which is $2\pi i\cdot\frac1{2i}=\pi$.

Answer 5

$\newcommand{\bbx}[1]{\,\bbox[15px,border:1px groove navy]{\displaystyle{#1}}\,} \newcommand{\braces}[1]{\left\lbrace\,{#1}\,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\,{#1}\,\right\rbrack} \newcommand{\dd}{\mathrm{d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,\mathrm{e}^{#1}\,} \newcommand{\ic}{\mathrm{i}} \newcommand{\mc}[1]{\mathcal{#1}} \newcommand{\mrm}[1]{\mathrm{#1}} \newcommand{\on}[1]{\operatorname{#1}} \newcommand{\pars}[1]{\left(\,{#1}\,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\root}[2][]{\,\sqrt[#1]{\,{#2}\,}\,} \newcommand{\totald}[3][]{\frac{\mathrm{d}^{#1} #2}{\mathrm{d} #3^{#1}}} \newcommand{\verts}[1]{\left\vert\,{#1}\,\right\vert}$ \begin{align} &\bbox[5px,#ffd]{\int_{-\infty}^{\infty} {\sin\pars{x} \over x}\,\dd x} = -\ic\,\mrm{P.V.}\int_{-\infty}^{\infty} {\expo{\ic x} \over x}\,\dd x \\[5mm] = &\ \ic\lim_{\epsilon \to 0^{+}}\int_{\pi}^{0}{\expo{\ic\epsilon\expo{\ic\theta}} \over \epsilon\expo{\ic\theta}}\,\epsilon\expo{\ic\theta}\ic\,\dd\theta = \ic\pars{-\ic\pi} = \bbx{\pi} \\ & \end{align}