Imagine a function that map (x,y) -> z
Imagine if we draw a bunch of curve where the value of z is the same. So that z is "potential field". The gradient is the steepest way to reach bottom.
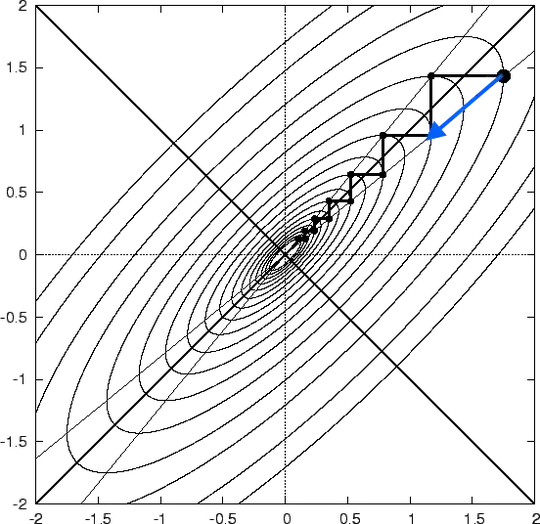
I found such pictures
Now, I am a bit confused with the picture.
The path perpendicular to the equipotential curves are indeed the black line. So that means if we want to go to steepest descent we must "zig zag". I must be missing something here
The gradient is NOT the direction that points to the minimum or maximum
I can see that it's an elipse. Say someone wants to go to the place with the lowest z (say in the middle), at the least distance possible, by following gradients. Which path he'll follow?
It looks like he'll follow the zig zag black path. After all at first point, the gradient does point to the left. Hmmm... But the blue path seems shorter.
How do we explain this?
What would be the path of always following gradient anyway for the corresponding graphs?