In this paper, page 92, the so called fundamental matrix in computer vision is derived.
Some notation:
$M = (x,y,z)^T$ is a 3d point and $ \left[ \begin{array}{cc} M\\ 1 \end{array} \right] $ represents the homogeneous coordinate $(x,y,z,1)^T$
There are two pinhole cameras defined as:
$P_i$ a 3x4 projection matrix for camera $i$:
$$m_i = P_i \left[ \begin{array}{cc} M\\ 1 \end{array} \right] = s_i \left[ \begin{array}{cc} u_i\\ v_i\\ 1 \end{array} \right]$$
The projection can be decomposed into $A_i\left[R_i\ t_i\right]$, where $A_i$ are the intrinsic parameters of the camera (an upper 3x3 triangular matrix), $R_i$ is a 3x3 rotation matrix (rotates the camera relative to the coordinate systems axises), and $t_i$ is a 3x1 translation vector. Note: $\left[R_i\ t_i\right]$ is a 3x4 matrix ($t$ is the last column).
$A_i$ defines the camera intrinsic parameters (focal length, scale factors, etc) I don't think these parameters are relevant to my question ,but the matrix looks like this:
$$ A_i = \begin{bmatrix}a&b&c\\0&d&e\\0&0&1\end{bmatrix} $$
The first camera ($i=1$) is positioned at origo and its axises aligns with the coordinate axises:
$$P_1 = A_1 \left[I\ \Bbb{0} \right]$$
The second camera is translated by $t$ and rotated by $R$ and has its own intrinsic parameters $A_2$:
$$P_2 = A_2\left[R\ t \right]$$
With these notations, we have the following two equations to project the 3d point $M$ to the plane of each camera:
$$ s_1m_1 = A_1[I\ 0] \left[ \begin{array}{cc} M\\ 1 \end{array} \right] \tag{1} $$ $$ s_2m_2 = A_2[R\ t] \left[ \begin{array}{cc} M\\ 1 \end{array} \right] \tag{2} $$
Epipolar geometry
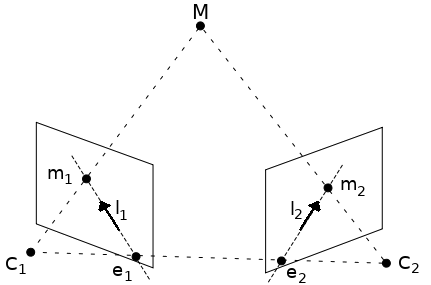
Given two images from two different cameras of the same scene, a ray from the camera center to a point $M$ will project as a line in each camera plane. $M$ is projected to $m_1$. There is a line $l_{m_1}$ in the other camera plane in which $m_2$ must be on. This line is called the epipolar line.
An image explains it better:
So if we know $m_1$, and we need to find $m_2$ (the corresponding point to $m_1$), then we could limit the search to the epipolar line $l_2$ (which goes through $e_2$ and $m_2$). In this way, we can search in one dimension instead of two for the corresponding points in the other camera image. Of course we cannot find $l_2$ via $m_2$ since we are looking for $m_2$.
The fundamental matrix $F$ is defined such that: $l_2 = F\ m_1$. And the constraint that $m_2$ will be on this line is: $m_2^T l_2 = 0$.
So the constraint to find $F$ is: $m_2^T F m_1 = 0$.
Unfortunately I'm not able to see (neither geometrically nor algebraically) how $F$ is derived / deduced.
Question
From these two equations, in the paper (and I've seen it in other papers as well), the following is deduced (which proofs the existence of $F$):
$$ m_2^{T}A_2^{-T}TRA_1^{-1}m_1= 0 $$
with the note: "by eliminating $M$, $s1$ and $s2$", and: $T$ is an antisymmetric matrix defined by $t$ such that, where $\times$ is the cross product, $Tx = t \times x$ for all 3D vectors.
How exactly can these be eliminated given (1) and (2)?
I thought I could eliminate $M$ this way:
$ A_2^{-1}s_2m_2 = RM+t $
$RA_1^{-1}s_1m_1 + t = RM+t$
$RA_1^{-1}s_1m_1 + t = A_2^{-1}s_2m_2$
At this point, I suppose T is used since $Tt$ would be $t$ cross $t$ which is zero.
$TRA_1^{-1}s_1m_1 = TA_2^{-1}s_2m_2$
Thankful for a hint or two.