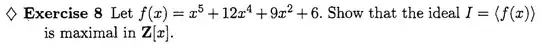2

In 'Fundamentals of Abstract Algebra' by Malik, Mordeson and Sen, at page $397$ the example no.$8$ shows that the ideal $\left<f(x)\right>$ is maximal in $\mathbb Z[x]$, where $f(x)$=$x^5$ + $12x^4$ +$9x^2$+$6$.

In solving the problem they have shown that $f(x)$ is irreducible, hence $\left<f(x)\right>$ is maximal. But we know that in a PID the an ideal is maximal iff it is generated by an irreducible element. Here $\mathbb Z[x]$ is not a PID. Also a generalized result is if $D$ is an Integral Domain, and $a$ is a non-zero element then $a$ is irreducible iff the ideal $\left<a\right>$ is maximal among all the principal ideals of $D$. But here the question is to show that $\left<f(x)\right>$ is maximal, so should I think that they wanted to show that $\left<f(x)\right>$ is maximal among all the principal ideals? Hope my confusion will be cleared. Thank you.

enter image description here enter image description here

user26857
  • 52,094
hiren_garai
  • 1,193
  • 1
    This does not seem right. See https://math.stackexchange.com/questions/740925/proof-for-maximal-ideals-in-mathbbzx. – lhf May 03 '17 at 12:48
  • Yes..but the problem is done in a renowned book ,so it's tough for me to conclude that it is wrong, that's why I asked .. – hiren_garai May 03 '17 at 12:51
  • @HirenGarai Is the print you are reading small enough to provide in a picture? – rschwieb May 03 '17 at 13:01
  • 1
    @HirenGarai Well... if this book is renown, then most books are renown... – rschwieb May 03 '17 at 13:05
  • @HirenGarai It could be an error, or it could be a misprint, an unclear statement, or else a misunderstanding by the reader. It's hard to say without access to the text. – rschwieb May 03 '17 at 13:06
  • 2
    @rschwieb, I've added the exercise in question. The first sentence of the solution is wrong. They probably mean $\mathbb Q[x]$ is the statement of the exercise. – lhf May 03 '17 at 13:11
  • @HirenGarai Thanks lhf! There we go. Now there is no doubt: the printed statement of exercise 8 (and its proof as lhf indicates) are simply wrong. – rschwieb May 03 '17 at 13:13
  • 2
    I've never heard of Mordeson or any of his books, but this one is a rather huge, pretty renowed, mistake, and It can't even be thought it is a typo as $;\Bbb Z[x];$ is written several times... – DonAntonio May 03 '17 at 13:26
  • I used to think only high school math books were crappy (meaning containing obvious mistakes) , but the story appears to be similar even for books meant for undergraduate courses. – Paramanand Singh May 04 '17 at 03:11

1 Answers1

3

$x^5 + 12x^4 +9x^2+6$ is irreducible in $\mathbb Z[x]$ because it is irreducible mod $5$ (according to WA).

This implies that $(5,x^5 + 12x^4 +9x^2+6)$ is a maximal ideal.

In particular, $(x^5 + 12x^4 +9x^2+6)$ is not a maximal ideal.

In general,

Every maximal ideal in $\mathbb{Z}[x]$ has the form $(p, f(x))$ where $p$ is a prime and $f$ is a primitive polynomial that is irreducible modulo $p$.

lhf
  • 216,483
  • Then why are they saying that $<f(x)>$ is maximal? Are they wrong ? – hiren_garai May 03 '17 at 12:53
  • @HirenGarai, the book is wrong. – lhf May 03 '17 at 13:08
  • The book is indeed wrong. The author was too hasty and thought that $\Bbb{Z}[x]$ was a PID. In the case of a PID any irreducible element generates a maximal ideal. See:

    https://math.stackexchange.com/questions/69814/is-the-ideal-generated-by-irreducible-element-in-principal-ideal-domain-maximal

     – Chickenmancer May 03 '17 at 13:23
  • One more thing in a pid an ideal generated by an irreducible elemnt is maximal is fine but in an id if an ideal is maximal then is it necessary that it is not generated by an irreducible elemnt?@Ihf – hiren_garai May 03 '17 at 13:24
  • No, take $\Bbb{Z}[x],$ it's an integral domain. The ideal $(2,x)$ is not principle, and not generated by an irreducible element, but it is prime, and it is maximal. – Chickenmancer May 03 '17 at 23:21
  • It is easy to prove that ideals of the form $(p, f) $ are maximal by realizing the quotient to be $\mathbb{Z}_{p} [x] /(f) $. But how do we prove the statement at the end of your post. Like given a maximal ideal $I$ of $\mathbb{Z} [x] $ how do I find $p, f$ from $I$? – Paramanand Singh May 04 '17 at 03:15