Let us take an arbitrary point $A_1$ on the circle. Now, the task is to choose $(n-1)$ points $A_2,...A_n$ on the circle which are chosen in such a way that lines $A_1A_2,...,A_1A_n$ divide the corresponding disk into $n$ parts of equal area.
How to prove that this is always possible?
This seems intuitively so obvious but is there some, preferably simple way, to prove it?
We need not to construct the points $A_2,...A_n$, just prove that they exist.
You can argument by induction, maybe? The following is not so rigorous, but I hope it gives a hint:
1) given a point $P$ on the circle, you can always divide the disc in two equal parts by a line passing through $P$: take the diameter passing through $P$.
2) Suppose you can divide the disk in $n$ equal parts. That means that there are $n$ points on the circle, $Q_1,Q_2,\dots,Q_n$ such that the lines $PQ_1, PQ_2,\dots PQ_n$ do the job. Let $A_n$ be the area of each part. If we add a point, we'd like to have $n+1$ points on the circle whic divide the disk in $n+1$ equal parts, each with area $A_{n+1} = \frac{n}{n+1} A_n$. To make room for the point $Q_{n+1}$, we have to shift each other point in such a way that each old area ($A_n$) decreases by a quantity proportional to $\frac{1}{n(n+1)}$. This is always possible because moving points along the circle in a continuous way is possible and the corresponding areas decrease in a continuous way.
If the disk has an area $A$ we need to divide him into $n$ parts, each of area $\dfrac {A}{n}$. Now choose point $A_2$ anywhere you want. If the line $A_1A_2$ divides disk into two parts, one with area $\dfrac {A}{n}$ and other with area $\dfrac {(n-1)A}{n}$ then we are done with $A_2$ and proceed to the point $A_3$. But if $A_1A_2$ divides disk into two parts, none of which has an area $\dfrac {A}{n}$ then it could be that "left" part of the disk has an area less than $\dfrac {A}{n}$ , but then we move point $A_2$ on the circle until we arrive at the point where one of the parts has an area $\dfrac {A}{n}$ and such point exists because if we move the point $A_2$ in such a way that "left" part of the disk has an area bigger than $\dfrac {A}{n}$ then because of the continuity of the "change of areas of the two parts of the disk when point $A_2$ travels on the circle" we must by some intermediatevaluedness have that there must exist point $A_2$ which divides disk into two parts, one with area $\dfrac {A}{n}$ and other with area $\dfrac {(n-1)A}{n}$. Now we apply the same procedure with all other points. This can be made more rigorous, of course, and more formal.
Without loss of generality let us assume that the radius of the circle is $1$, that said circle is centered at $O = (0,0)$ and that $A_1 = (1,0)$.
We will show that one can divide the upper half disk in $n$ equal parts. If one wishes to divide the whole disk in $n$ equal parts just mirror the "cuts" in the upper half disk and group the pieces in pairs.
Finding $A_k$ is equivalent to find the angle $\theta_k = \angle A_kOA_1$ such that the area of the corresponding sector minus the area of the triangle $A_1OA_k$ is $\frac{k}{n}\pi$.
The area of the sector is $\frac{\theta_k}{2\pi}\pi = \theta_k/2.$ We can divide the triangle $A_1OA_k$ into two congruent triangles $A_1OB$ and $A_kOB$ where $B$ is the projection of $O$ into the segment $A_1A_k$.
Note that this are two right triangles and $\angle BOA_1 = \angle BOA_k = \theta_k/2$, so the area of each triangle is $\frac{1}{2}\sin(\theta_k/2)\cos(\theta_k/2)$ and since we have two of them, the total area is $\dfrac{1}{2}\sin(\theta_k)$.
In other words,
$$\tag{*}\dfrac{k}{n}\cdot\dfrac{\pi}{2} = \dfrac{\theta_k - \sin(\theta_k)}{2}.$$
To prove that such a $\theta_k$ exists, note that the function $A(\theta) = \dfrac{\theta - \sin(\theta)}{2}$ is a continuous and strictly increasing function in $(0,\pi)$ since its derivative is $(1-\cos(\theta))/2 > 0$.
Also $A(0) = 0$ and $A(\pi) = \pi/2$, so by continuity, a unique $\theta_k$ exists in $(0,\pi)$ for all $0 < k < n$ that satisfies $(*)$. When $k = n$ then $\theta_n = \pi$.
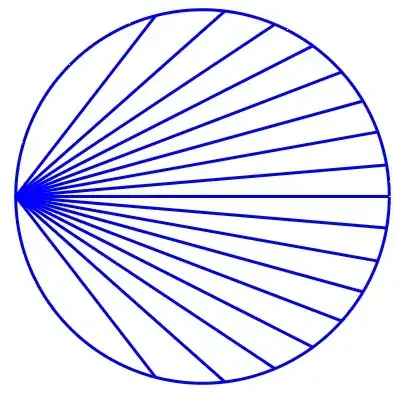
WLOG we can work with the unit circle $S_1$ with point $P(-1,0)$.
The polar equation of $S_1$ with respect to pole $P$ is
$$\tag{1}r=r(\theta)=2 \cos(\tfrac{\theta}{2}), \ \ 0 \leq \theta \leq \pi.$$
Remark: in this way, due to the inscribed angle theorem (see Euclid's proof in (http://aleph0.clarku.edu/~djoyce/java/elements/bookIII/propIII20.html)), $\theta$ can be interpreted as the reference angle with respect to the center $O$ of $S_1$.
The sector area between $\theta_1$ and $\theta_2$ is known to be
$$\tag{2}A_{\theta_1,\theta_2}=\tfrac12 \int_{\theta_1}^{\theta_2}r(\theta)^2d\theta=\int_ {\theta_1}^{\theta_2}2\cos(\tfrac{\theta}{2})^2d\theta =\int_{\theta_1}^{\theta_2}(1+\cos(\theta))d\theta = [\theta+\sin(\theta)]_{\theta_1}^{\theta_2}$$
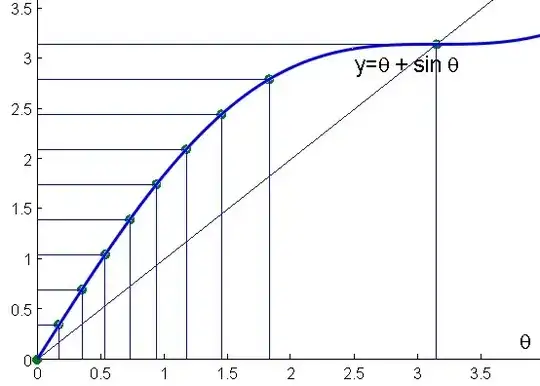
Let us define function $\varphi$ by
$$\tag{3}\varphi(\theta):=\theta+\sin(\theta).$$
Thus, (2) becomes:
$$\tag{4}A_{\theta_1,\theta_2}=\varphi(\theta_2)-\varphi(\theta_1).$$
$\varphi$ is increasing from $0$ to $2 \pi$ because it has a positive derivative.
It suffices now to subdivide interval $[0,2\pi)$ with values
$$\tag{5}\theta_k:=\varphi^{-1}(\tfrac{2\pi k}{n}).$$
Remark: $\varphi^{-1}$ has no explicit expression (Inverse of $f(x)=\sin(x)+x$), but is connected to a form of Kepler's equation (https://en.wikipedia.org/wiki/Kepler%27s_equation) and to cycloids.
Therefore, we cannot hope to have exact values for the $\theta_k$s. Only a numerical approach is possible. Fotunately, this issue can be solved by the very simple fixed point method. Indeed, as (5) is equivalent to:
$$\tag{6}\theta+\sin(\theta)=\tfrac{2\pi k}{n}$$
itself equivalent to:
$$\tag{7}\theta=A-\sin(\theta), \ \ \ \text{with} \ \ \ A:=\tfrac{2\pi k}{n},$$
the solution $x$ of (7) will be obtained as the limit of the fixed-point iteration sequence :
$$\tag{8}\theta_{i+1}=A-\sin(\theta_i) \ \ \ \text{with} \ \ \ \theta_0=A.$$
(the convergence is granted by the fact that the derivative of the function in the RHS of (8) is $<1$ in open intervals around the roots we are looking for.)
