2

Consider three concentric circles with center O and radii 1,2 and 3 respectively.

Consider point A on the circle of radius 1, B on the circle with radius 2 and C on the circle with radius 3.

  1. What is the expected area of △ABC?
  2. What is the maximum area of △ABC?

I have tried assigning complex numbers to coordinates, proceeding by fixing angles, but nothing seems to work.

katarasaang
  • 15
Michael Klyachman
  • 180
  • The fact that you seem to repeat twice every number and letter makes it hard to read. – Zubzub May 02 '17 at 12:27
  • Radii $22$ and $33$ in your text are in fact $2$ and $3$, Right ? – Jean Marie May 02 '17 at 12:37
  • You mean "unsigned areas" , of course, otherwise the mean would be 0... – Jean Marie May 02 '17 at 12:39
  • I have corrected your text. Do you agree ? – Jean Marie May 02 '17 at 12:41
  • Seems like the "maximum area" is solved over there: https://math.stackexchange.com/questions/177213/maximum-area-of-a-triangle (haven't read it) – N.Bach May 02 '17 at 12:43
  • Everything can be tackled by a choosing a suitable parametrization depending on two angles (like $\widehat{AOB}$ and $\widehat{BOC}$) and by applying the sine theorem. The most difficult part is just to deal with configuration issues, related with the cases in which $O$ lies outside $ABC$. – Jack D'Aurizio May 02 '17 at 12:51
  • About the maximum area: if $ABC$ has maximum area, $AO\perp BC$ and so on, hence $O$ is the orthocenter of $ABC$. The distances of the orthocenter from the vertices in a general triangle are simple to compute. – Jack D'Aurizio May 02 '17 at 12:56

1 Answers1

1

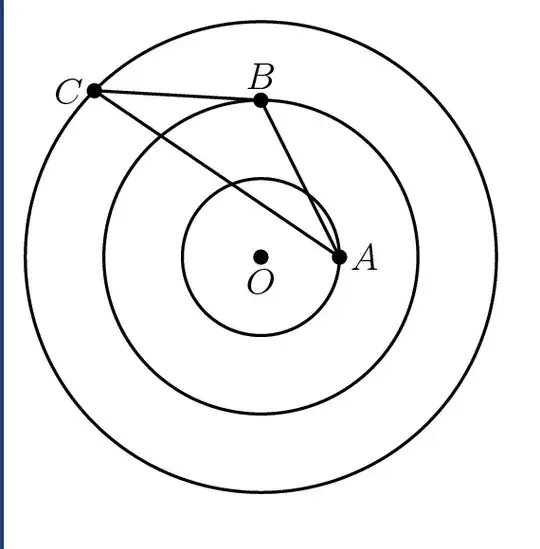
Assume uniform distribution for the point on each circle. We can fix one of the points because area is rotationally invariant. Fix the inner most point to be $(1,0)$.

Denote $x$ and $y$ the phase angles of the points on the circles with radii $2$ and $3$ respectively. Using a formula for the area of a triangle given the cartesian coordinates of its vertices we get that the expected area is

$$\frac{1}{8\pi^2}\int_0^{2\pi}\int_0^{2\pi}\left|2\sin\left(x\right)-3\sin\left(y\right)+6\cos\left(x\right)\sin\left(y\right)-6\cos\left(y\right)\sin\left(x\right)\right|dxdy$$

$$\approx 2.0829$$

UPDATE:

The formula for the area of triangle $(A, B, C)$ is

$$\frac{|A_x(B_y-C_y) + B_x(C_y-A_y) + C_x(A_y-B_y)|}{2}$$

We have $A=(1,0)$, $B=2(\cos(x), \sin(x))$ and $C=3(\cos(y), \sin(y))$. A factor of $\frac{1}{2\pi}$ comes from the uniform distribution for both $x$ and $y$. (We also assume independency.) Just place the values for the point coordinates in and the formula follows. (Notice, how the values $A_x=1$ and $A_y=0$ simplify the formula.)

For the maximum area, Wolfram Alpha gives $4.90482$ at $x=2.3882$ and $y=4.2046$. I don't know if exact forms can be found.

ploosu2
  • 8,707
  • Could you derive your formula in steps? – cis Jul 11 '19 at 20:45
  • @cis I updated my answer, but there actually aren't that many steps, it is just the application of the shoelace-formula, as it is called. For its derivation see for example here: https://math.stackexchange.com/questions/516219/finding-out-the-area-of-a-triangle-if-the-coordinates-of-the-three-vertices-are – ploosu2 Jul 14 '19 at 17:40
  • Ok, I think I understand more. A question: Why don't you place $A=(0,0)$? – cis Jul 14 '19 at 19:01
  • @cis It's easier to have the center of the circles in the origin, so they have the parametrization $r(\cos(t), \sin(t))$. – ploosu2 Jul 15 '19 at 06:56
  • Ah yes, I understand. – cis Jul 15 '19 at 18:54