6

So the problem deals with a chain at a fixed length, bends but does not stretch under gravity.

The total graviational potential energy is $$g\rho\int y\sqrt{1 + y^{'2}}dx$$

Where $g$ is gravity.

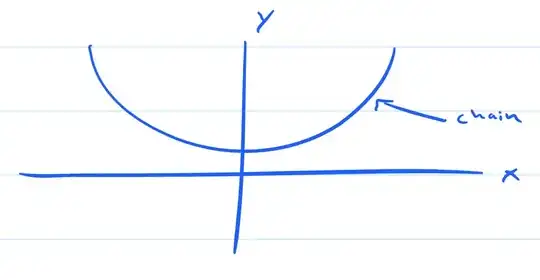
The problem has a picture of the chain on the xy plane enter image description here

So what I want to know is how to derive the equation using the drawing. It's to my limited understanding that the square root $\sqrt{1 + y^{'2}}$ is describing a segment on the curve but what exactly is the $y$ representing in the picture? And how $mgh$ translates to the equation?

Also any help on arriving to the solution $y = coshx$ would be greatly appreciated but I am more interested on the equation right now.

stack ex
  • 350

2 Answers2

8

The mass in $mgh$ is locally $dm=\rho\,ds$, where $\rho$ is the lineic mass and $ds$ the element of length, also written $ds=\sqrt{dx^2+dy^2}=dx\sqrt{1+y'^2}$.

Hence the total energy (with $h\equiv y$)

$$\rho g\int y\sqrt{1+y'^2}dx.$$

By the Euler-Lagrange equation,

$$\frac{\partial f}{\partial y}=\frac{d}{dx}\frac{\partial f}{\partial y'},$$

i.e.

$$\sqrt{1+y'^2}=\frac{d}{dx}\frac{yy'}{\sqrt{1+y'^2}}=\frac{y'^2+yy''}{\sqrt{1+y'^2}}-\frac{yy'^2y''}{(1+y'^2)^{3/2}},$$

$$(1+y'^2)^2=(y'^2+yy'')(1+y'^2)-yy'^2y'',$$

$$1+y'^2-yy''=0,$$ $$\frac{y'}y-\frac{y'y''}{y'^2+1}=0,$$ $$(\log y)'=\left(\frac12\log(y'^2+1)\right)',$$ $$Cy^2=y'^2+1,$$ $$\frac{y'}{\sqrt{Cy^2-1}}=1$$ and finally

$$\frac1{\sqrt C}\text{arcosh}\sqrt Cy=x+C'$$

  • 2
    you are not using the constraint that the lenght of the chain is fixed. It can be introduced with a Lagrange mutliplier. – J. R. C. Feb 21 '20 at 11:38
2

You more or less already answered it: You need to understand how mgh translates. So \rho = m and y = h and the g is already in the Formula. Work = Force *segement and the Energy is an integrated version of this.

For getting the minimizer you might try the Euler-Lagrange Equations.

Hasenkoettel
  • 21