1

I've come across the statement which says that if two events $A$ and $B$ are disjoint, then they are dependent because if, for example, $A$ occurs, it gives us the information that $B$ didn't occur. So far so good.

Hence I draw the conclusion (possibly erroneously) that if two events are not disjoint, they are independent.

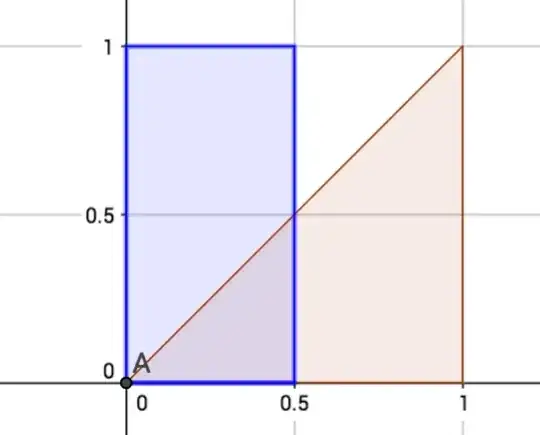
I'm trying to test it with the artificial example a friend of mine came up: Sample space: unit square

Consider the sample space in the picture which is the unit square.

Event $A$ - the blue rectangle

Event $B$ - the brown triangle

$P(A)=0.5$

$P(B)=0.5$

$P(A\cap B)=0.125$

Obviously, $P(A)*P(B)\neq P(A\cap B)$ and I conclude that $A$ and $B$ are also dependent.

So, I am wrong saying that if $A$ and $B$ are not disjoint, they are always independent?

alekscooper
  • 952
  • @Lazy Lee Nope, because if $A$ and $B$ are disjoint, they are dependent, but if they are not disjoint, does it mean that they are independent?

    I know that my example does contradict that, but does it exhaust all the possible cases?

     – alekscooper May 02 '17 at 08:11
  • 1
    Yes, you are wrong in saying that. Compliments for your friends example. – drhab May 02 '17 at 08:11
  • 1
    Another thing: "If $A$ occurs then it gives us the information that $B$ didn't occur..." Yes, but that information is useless if the probability that $B$ will occur is $0$. (see also the answer of Mees). – drhab May 02 '17 at 08:27
  • My final paragraph here offers two examples of non-disjoint pairs of events: the first pair is independent, while the second pair is dependent. In short: dependence/independence cannot be inferred from non-disjoint events. – ryang Apr 03 '22 at 12:40

2 Answers2

2

Yes, you are wrong in saying that, as your example demonstrates.

Note that disjoint does not imply dependent in an general either: if $A = \emptyset$, then $$ P(A \cap B) = P(\emptyset) = 0 = 0\cdot P(B) = P(\emptyset)P(B) = P(A)P(B), $$ so the empty set is disjoint from every set, and also independent from every set.

Mees de Vries
  • 26,947
0

This seems to be more of a logical fallacy than anything else.

Disjoint $\Rightarrow$ Dependent is not logically equivalent to

Not Disjoint $\Rightarrow$ Not Dependent.

What you have, however, is that it is logically equivalent to

Not Dependent $\Rightarrow$ Not Disjoint.

This is a special case of a general rule which asserts that a conditional statement is logically equivalent to its contrapositive.

You can read more about this on https://en.wikipedia.org/wiki/Contraposition

Improve
  • 1,788