Consider a sequence of length $s+m$ with $s$ successes and $m$ failures in total.
You know that the number of such sequences is given by ${{s+m} \choose m} $, and that each has a probability of $p^s (1-p)^{m}$
A sequence as above can be considered a binary string of length $s+m$, with $s$ ones in total.
Now you can refer to the answers to this other post [ number of occurrences of k consecutive 1s in a binary string of length n ]
(http://math.stackexchange.com/questions/2045496)
where it is explained that
the number of binary strings with $s$ 1's, $m$ 0's, and which contains runs of consecutive 1's of length at most $r$ is
given by
$$
N_b (s,r,m + 1) = {\rm No}{\rm .}\,{\rm of}\,{\rm solutions}\,{\rm to}\;\left\{ \matrix{
{\rm 0} \le {\rm integer}\;x_{\,j} \le r \hfill \cr
x_{\,1} + x_{\,2} + \; \cdots \; + x_{\,m + 1} = s \hfill \cr} \right.
$$
where $N_b (s,r,m + 1) $ is expressible by the sum
$$ \bbox[lightyellow] {
N_b (s,r,m + 1)\quad \left| {\;0 \le {\rm integers }s,m,r} \right.\quad = \sum\limits_{\left( {0\, \le } \right)\,\,k\,\,\left( { \le \,{s \over r}\, \le \,m + 1} \right)} {\left( { - 1} \right)^k \left( \matrix{
m + 1 \cr
k \cr} \right)\left( \matrix{
s + m - k\left( {r + 1} \right) \cr
s - k\left( {r + 1} \right) \cr} \right)}
}$$
So we conclude that
the probability of having at most $r$ consecutive successes in $n$ Bernouilli trials,
each with success probability $p$
is given by
$$ \bbox[lightyellow] {
P_{\,M}(r,p,n) = \sum\limits_{0\, \le \,\,s\,\, \le \,n} {p^{\,s} \left( {1 - p} \right)^{\,n - s} \sum\limits_{\left( {0\, \le } \right)\,\,k\,\,\left( { \le \,{s \over r}\, \le \,n - s + 1} \right)} {\left( { - 1} \right)^k \left( \matrix{
n - s + 1 \cr
k \cr} \right)\left( \matrix{
n - k\left( {r + 1} \right) \cr
s - k\left( {r + 1} \right) \cr} \right)} }
}$$
while instead
the probability of having at least $r$ consecutive successes in $n$ Bernouilli trials,
each with success probability $p$
(the one you are looking for) is clearly
$$ \bbox[lightyellow] {
P_{\,L} (r,p,n) = 1 - P_{\,M} (r - 1,p,n)
}$$
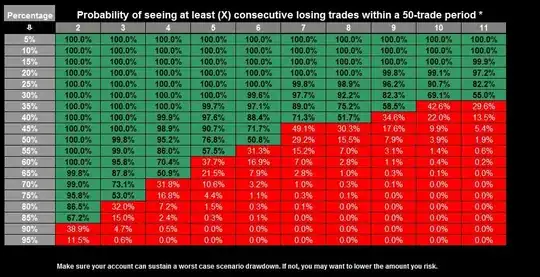
For example, with a win probability of $0.9$ (thus loss $=0.1$) the probability of having at least $2$ consecutive
losses (successes) in $50$ tradings will be
$$
P_{\,L} (2,0.1,50) = 1 - P_{\,M} (1,0.1,50) = 0.36367...
$$
as correctly pointed out by Henry.
Some other values are given in this table (here p = win)
$$
\begin{array}{l}
P_{\,L} (r,\;1 - p,\;50) \\
\begin{array}{c|ccc}
\hline
{p\backslash r} & & 2 & 3 & 4 \\
\hline
{0.3} & & {1.0} & {1.0} & {0.9978} \\
{0.5} & & {1.0} & {0.9827} & {0.8274} \\
{0.8} & & {0.8202} & {0.2707} & {0.059} \\
{0.9} & & {0.3634} & {0.0425} & {0.0042} \\
\end{array} \\
\end{array}
$$
Also, putting $r=2 \; p (win)=0.9$ and $n=0,1,2,..$, it is easy to check that we obtain the values already indicated
by Henry at the end of his answer.
And to satisfy your curiosity, $P_{\,L} (15,\;0.55,\;500) = 0.0275867...$ again confirming Henry's answer.
However, for large $n$ an asymptotical formula would be needed, which at the moment I did not succeed and find.
calc_prob(n_trades=20000, x_loses=13, probability=0.4). def calc_prob(n_trades, x_loses, probability): # Initial values gn = [1] fn = 0 for trade in range(1, n_trades + 1): # Calculate actual G(n) g_num = trade - x_loses gna = probability * (1 - fn) gn.append(gna) gna = gn[g_num] if g_num >=0 else 0 # Calculate actual F(n) fn = fn + ((1 - probability)*x_loses) float(gna) ret – Michal Gow Feb 15 '19 at 12:16