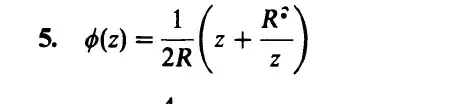Conformal Mapping #5

Question

I am studying for my final exam and am really struggling on this question #5. I have attached both the question and the answer listed in the book. I am really trying to get the ideas down so that I do well on the final.

My attempt (Finding a conformal map of the part of the upper half-plane outside a circle of radius r onto the entire upper half plane):

I want to use a known conformal map to map the domain to the first quadrant. I then want to use w=z^2 to map to the first quadrant to entire half plane. Finally I want to use a linear fractional transformation that maps the upper half-plane to itself. The only thing is I don't know how to map the domain to the first quadrant and what the linear fractional transformation should be, but this is my general idea that I am thinking.

Any help, suggestions, tips would be much welcomed, as I am struggling with these concepts.

My thinking is this: your (5.) is half of an outer annulus. The reciprocal map should take your region and make it into a half disk. Then, dilate to the unit half disk and use one of your standard maps to go from half disk to half plane. Pick three convenient points and set-up the fractional linear transformation to make that map from the half disk to the half plane... this is a sketch, I might be missing something without fleshing out the details. I bet someone works this one out for you, it sounds fun. — James S. Cook, Apr 28 '17 at 00:25
@JamesS.Cook Good idea. You should write it up as an answer. — zhw., Apr 30 '17 at 16:27
Related : In which sense does Cauchy-Riemann equations link complex- and real analysis? , Potential flow around a circular cylinder , a problem in application of conformal mappings . — Han de Bruijn, Apr 30 '17 at 18:18
Related : Potential flow around a circular cylinder , as has been used (again) as an example in : Solving for streamlines from numerical velocity field . — Han de Bruijn, Apr 30 '17 at 18:20

score 3 · Answer 1 · answered May 05 '17 at 19:49

I think you and @JamesS.Cook have some good ideas. Here's what I would do: i) $z\to z/R$ normalizes the situation. ii) the map $z\to 1/z$ then takes the exterior of the upper unit half disc to the lower unit half disc. iii) follow that with the map $z\to -z.$ Now we're in the upper unit half disc.

Now, my favorite go-to map from the full open unit disc to the right half plane is

$$z\to \frac{1+z}{1-z}.$$

This map will take the upper unit half disc to the first quadrant as you wanted. Now apply $z\to z^2$ to arrive at the final map.

Putting that together gives the map

$$f(z) = \left (\frac{z-R}{z+R}\right)^2.$$

Now that doesn't look like your map, but there are a lot of bilholomorphic self maps of the upper half plane, for example $-1/z, az$ for $a>0$ and $z+b$ for $b\in \mathbb R$ and compositions of such. So one of those composed with $f$ should give your map.

Conformal Mapping #5

1 Answers1