-3

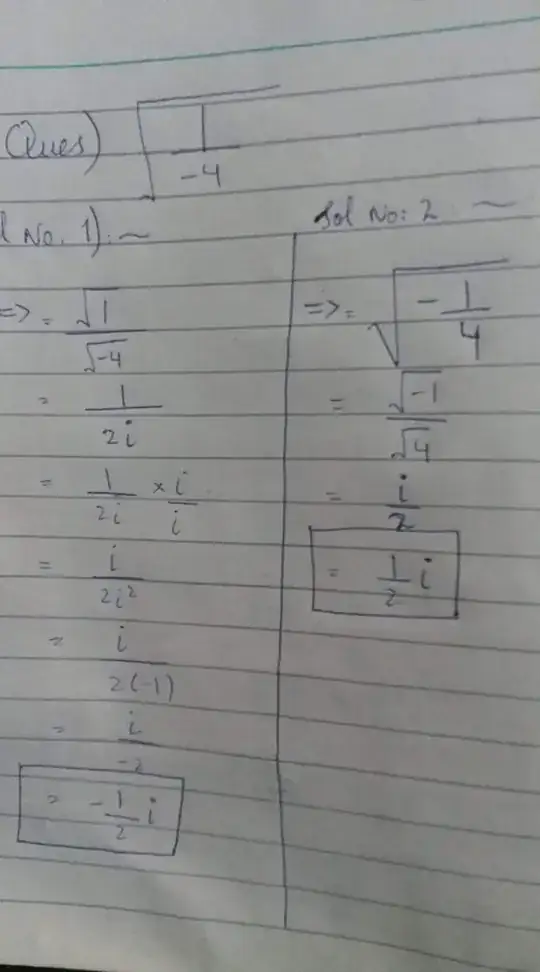
enter image description here which solution is correct in the picture?

Umar
  • 56
  • 2
  • 1
    Technically, the notation given problem is "ambiguous" but I am pretty sure that they mean the boxed answer on the right. Not that I agree though... – imranfat Apr 27 '17 at 21:06
  • @imranfat: Keyphrase "principal value" –  Apr 27 '17 at 21:07
  • I find the downvotes on the question surprising. –  Apr 27 '17 at 21:09
  • I agree, and I did not downvote on this post... – imranfat Apr 27 '17 at 21:12
  • Why do you find the downvotes surprising, @Hurkyl? Mind you, my votes (up and/or down) expired for the day before this question was even posted.) But I certainly find nothing whatsoever surprising about the downvotes here. The only characters the OP entered are <which solution is correct in the picture?> (barely enough characters, mind you, to get past the minimum character requirement). Hardly the kind of question that is described in "how to ask a good question" (help section). – amWhy Apr 27 '17 at 21:25

2 Answers2

2

Both.

There are two square roots for every non-zero number. Try squaring either answer.

Updated to reflect Matt Samuel's valid point.

Jed
  • 86
  • This problem is not about finding "squareroots" This problem is about taking the squareroot as an operator... – imranfat Apr 27 '17 at 21:07
  • @imranfat: And often, $\sqrt{}$ is meant to refer to a multi-valued operator, or an indeterminate choice of single-valued operator, rather than a specific single-valued one. –  Apr 27 '17 at 21:08
  • 1
    @Hurkyl A better way is stating "Solve the equation $x^2=-1/4$. Then there are two square roots – imranfat Apr 27 '17 at 21:09
  • The principal root is only defined for positive real numbers: http://mathworld.wolfram.com/PrincipalSquareRoot.html – Jed Apr 27 '17 at 21:09
  • 1
    @Jed Not all universities agree on that notion about the particular squareroot symbol. We explicitly avoided negative numbers under the squareroot and referred to the polynomial equation from where we calculated all its roots – imranfat Apr 27 '17 at 21:10
  • 1
    $0$ has only one square root. – Matt Samuel Apr 28 '17 at 05:50
1

Both answers are correct. Square root of any complex number always has two values. Generally speaking, the equation $x^n = a$ has exactly $n$ roots for any complex $a$.

Consider reading about root of unity: article.

Ramil
  • 1,882
  • Could you expand on your first two sentences, Ramil? Otherwise it could easily qualify as a link only answers. It is important that answers not depend on an explanation in a link; rather, a summary of the argument in the link should be provided directly within an answer. (Links, over time, aren't reliable.) – amWhy Apr 27 '17 at 21:19
  • 1
    @amWhy Thanks, I expanded the answer a little. – Ramil Apr 27 '17 at 21:41
  • That helps a lot! – amWhy Apr 27 '17 at 21:44
  • 2
    I'm out of votes for the day, but I'll try to keep the tab open to this question (and answers) long enough (the next 2hours and 15 minutes, until the "new" MSE day), so I can upvote your answer then. – amWhy Apr 27 '17 at 21:46
  • @amWhy Ok, thanks! :) – Ramil Apr 28 '17 at 21:07
  • There you go, Ramil! – amWhy Apr 29 '17 at 00:03