2

Background: This "identity" (if it is one) is motivated by Harris Mathematics for Physical Science question 2.5.4 asking to produce the series for 1/sin(x).

The integral of $\csc(x)$ is $-\ln|\csc(x)+\cot(x)|$, I have never seen it given as $\log(\tan(x/2)$. What identity converts one into the other? 

series = Integrate[Series[Csc[x], {x, Pi/2, 10}], x]
series2 = Series[Log[Tan[x/2]], {x, Pi/2, 12}]

enter image description here

If you plot them with wolfram alpha you might be confused because the imaginary graph displays different branches of the log function for the two, but they are the same. 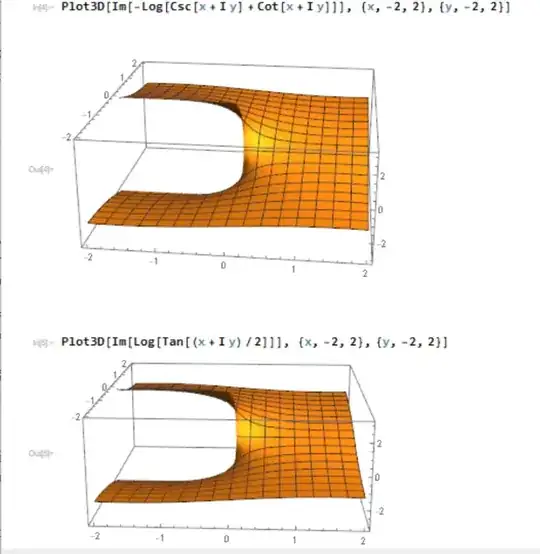enter image description here What likely simple identity am I forgetting or not understanding? Putting the $-\ln|\csc(x)+\cot(x)|$ over a common denominator I think I get $-\ln\mid\frac{2}{\sin(2x)}\mid$

user5389726598465
  • 1,171

1 Answers1

3

Hint: $$ \tan\left(\frac x2\right)=\frac{\sin(x)}{1+\cos(x)}=\frac1{\csc(x)+\cot(x)} $$ The first identity is shown in this answer.

robjohn
  • 345,667