5

I saw this problem in a puzzle book. Just wondering if anyone can explain the principle behind this method.

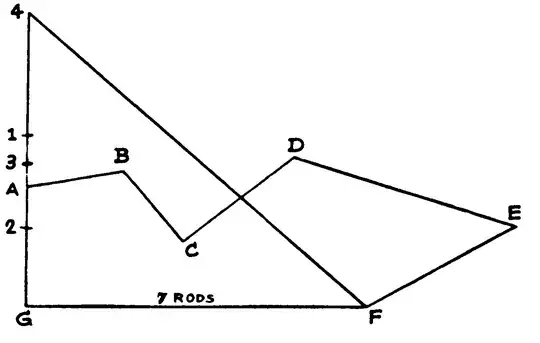
A rectilinear figure of any number of sides can be reduced to a triangle of equal area, and as $\angle AGF$ happens to be a right-angle the thing is quite easy in this way:

  • Continue the line $GA$.

  • Now lay a parallel ruler from $A$ to $C$, run it up to $B$ and mark the point $1$.

  • Then lay the ruler from $1$ to $D$ and run it down to $C$, marking point $2$.

  • Then lay it from $2$ to $E$, run it up to $D$ and mark point $3$.

  • Then lay it from $3$ to $F$, run it up to $E$ and mark point $4$.

If you now draw the line $4$ to $F$ then $\triangle G4F$ is equal in area to the irregular field.

As our scale map shows $GF$ to be $7$ inches (rods), and we find the length $G4$ in this case to be exactly $6$ inches (rods), we know that the area of the field is $\frac 12 (7\times 6)$ or $21$ square rods.

enter image description here

The simple and valuable rule I have shown should be known by everybody-but is not

Community
  • 1
Peter
  • 366

1 Answers1

2

It is the standard Euclidean procedure for reducing any polygon to a triangle.

Take triangle ABC (yellow) and triangle A1C (pink) as in the diagram below:

enter image description here

Since 1B and AC are parallel, the two triangles have the same area. Hence the polygon GABC... has the same area as G1C..., which is a polygon with one less vertex. Continuing like this reduces the original polygon to a triangle of the same area.

Chrystomath
  • 10,798