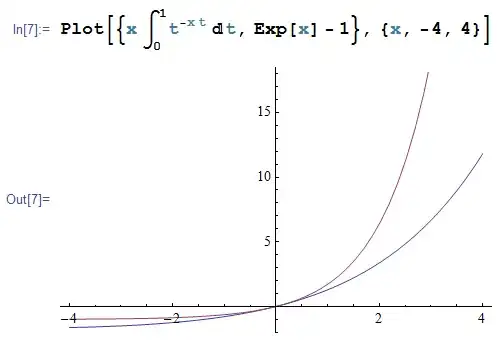5

When trying to prove, in this previous question, that $\sum_{n=1}^\infty \frac{x^n}{n^n}<0$ when $x<0$, a common fallacy is incited by the resemblance between the given summation and $\sum_{n=1}^\infty \frac{x^n}{n!}$:

Because $n^n\geqslant n!$ for $n\geqslant 1$,

$$\sum_{n=1}^\infty \frac{x^n}{n^n} \leqslant \sum_{n=1}^\infty\frac{x^n}{n!}=\left(\sum_{n=0}^\infty\frac{x^n}{n!}\right)-1=e^x-1.$$

Unfortunately, this proof only works for the case where $x\geqslant 0$, because the bounding on the summand doesn't hold for $x<0$ when the power $n$ is odd.

However, this invalid proof doesn't imply that $\sum_{n=1}^\infty \frac{x^n}{n^n} \leqslant e^x-1$ doesn't hold for $x<0$. As a matter of fact, we could observe the following figure, where the lower, $\color{blue}{\text{blue}}$ line is $$\sum_{n=1}^\infty \frac{x^n}{n^n}=x\int_0^1 t^{-xt}\,\mathbb dt,$$ and the higher, $\color{purple}{\text{purple}}$ line is $e^x-1$.

Comparing two plots

Therefore, how to prove that $\displaystyle\sum_{n=1}^\infty \frac{x^n}{n^n} \leqslant e^x-1$ for all $x\in\mathbb R$? (Equality holds at and only at $x=0$.)

Community
  • 1
Frenzy Li
  • 3,685
  • Alternating series remainder? – Simply Beautiful Art Apr 24 '17 at 12:01
  • 1
    I don't see why the bounding on the summand depends on wether $n$ is even or odd... – Peter Apr 24 '17 at 12:03
  • @Peter sorry, should be for odd powers. Well, $\frac{a}{n^n}\leqslant \frac{a}{n!}$ if and only if $a\geqslant0$. – Frenzy Li Apr 24 '17 at 12:04
  • @SimplyBeautifulArt Is there a reference for that? I don't recall anything from that... – Frenzy Li Apr 24 '17 at 12:05
  • @FrenzyLi If you have an alternating series $\sum_{n=1}^\infty a_n$ with $|a_n|$ nonincreasing then $\left | \sum_{n=1}^\infty a_n - \sum_{k=1}^N a_k \right | \leq |a_{N+1}|$. An analogue is true if $|a_n|$ is merely eventually nonincreasing (in which case $N$ needs to be chosen large enough that $|a_n| \geq |a_{n+1}|$ for all $n \geq N$). The latter is applicable here (I think the former is not). – Ian Apr 24 '17 at 12:16
  • @Ian Starting from $$\left|\sum_{n=1}^\infty \left(\frac{x^n}{n!}-\frac{x^n}{n^n}\right) - \sum_{n=1}^{N-1} \left(\frac{x^n}{n!}-\frac{x^n}{n^n}\right)\right| \leqslant \left|\frac{x^N}{N!}-\frac{x^N}{N^N}\right|\quad\text{?}$$ – Frenzy Li Apr 24 '17 at 12:29
  • 1
    A reformulation: $$e^x-1=\int_0^1 xe^{x t},dt\implies e^x-1-\int_0^1 xt^{-x t},dt=\int_0^1 x(e^{x t}-t^{-x t}),dt$$ so the claim is equivalent to this integral being positive. Rather amazingly, this integral has a closed-form solution according to Mathematica. – Semiclassical Apr 24 '17 at 13:26
  • My last statement in that comment should be disregarded: no such closed-form exists. (User error.) – Semiclassical Apr 24 '17 at 13:32

1 Answers1

0

Let us set $0^0=1$ just to simplify the notation.We have to prove that for any $x>0$ $$ \sum_{n\geq 0}\frac{(-1)^n}{n^n} x^n \leq e^{-x} \tag{1}$$ holds, or that $$ \sum_{n\geq 0}\frac{(-1)^n}{n^n}x^n\sum_{m\geq 0}\frac{1}{m!}x^m \leq 1 \tag{2}$$ holds. By writing the LHS of $(2)$ as a Cauchy convolution, we need to prove

$$ \sum_{l\geq 0}\left(\sum_{k=0}^{l}\frac{(-1)^k}{k^k (l-k)!}\right) x^l \leq 1 \tag{3}$$ or: $$ \sum_{l\geq 1}\left(\frac{1}{l!}+\sum_{k=1}^{l}\frac{(-1)^k}{k^k(l-k)!}\right)x^l\leq 0\tag{4}$$ and we may check by induction that the involved coefficients are all $\leq 0$.

Jack D'Aurizio
  • 353,855
  • How to prove the induction step, i.e. from $$\displaystyle\frac{1}{l!}+\sum_{k=1}^{l}\frac{(-1)^k}{k^k(l-k)!}\leq 0$$ to $$\displaystyle\frac{1}{(l+1)!}+\sum_{k=1}^{l+1}\frac{(-1)^k}{k^k(l+1-k)!}\leq 0\quad \text{?}$$ I keep trying to bound each term but then realize that $(-1)^k$ can be negative... – Frenzy Li Apr 24 '17 at 15:00