Order preserving map $\mathbb R^2 \mapsto \mathbb R$

Question

What would be an order preserving map $\mathbb R^2 \mapsto \mathbb R$ if $\mathbb R^2$ is arbitrarily ordered by x then y?

I saw the interleaving answers here: Examples of bijective map from $\mathbb{R}^3\rightarrow \mathbb{R}$ but they don't mention order preserving.

Simply doing a linear transofrmation $w=5x+7y$ for example isn't order preserving because before $(1,1) < (2,0)$ but after $12 > 10$.

So what would be an order preserving map? Is interleaving order preserving?

Edit: By arbitrarily ordering $\mathbb R^2$ I mean using a comparer like this one:

(a,b)=>{  //a,b are Vector2
    let x = a.x - b.x;
    if (x != 0){
        return x;
    }
    return a.y - b.y;  // a tie with x is broken with y
}

So for example $(1,3) < (1,5) < (2,2)$

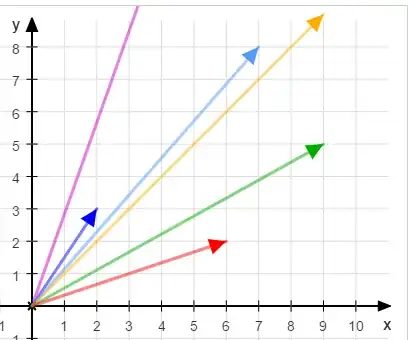
Another comparer is to set a known minimum point and then to compare distances from that point. My set of points is known to be "larger" than that minimum.

For example:

I set my minimum to $(0,0)$ and then order all the other points relative to their distance from that point. So we'll get: blue(2,3) < red(6,2) < green(9,5) etc.

If you mean an injective order preserving map, there is no such map. — Crostul, Apr 24 '17 at 11:19
Even if $\mathbb R^2$ is arbitrarily ordered by x then y? @Crostul — shinzou, Apr 24 '17 at 11:20
"arbitrarily ordered by x then y" is not clear: what do you mean? I mean lexicographic order. — Crostul, Apr 24 '17 at 11:21
I added a code example, I think it's the best explanation. @Crostul — shinzou, Apr 24 '17 at 11:25
If there is an order on $\mathbb{R}^{2}$ then that order map will act as the order preserving map. — awCwa, Apr 24 '17 at 11:53
Then doing a linear transformation on it with a monotone increasing function like I've shown should preserve that order, but it doesn't. @SivaKumar — shinzou, Apr 24 '17 at 12:05
How do you prove that linear transformation is a monotone function on $\mathbb{R}^{2}$ with respective the order given. — awCwa, Apr 24 '17 at 12:27
It's a straight line equation. I also added another comparer in the question. @SivaKumar — shinzou, Apr 24 '17 at 12:30

egreg · Accepted Answer · 2017-04-24T17:05:53.427

4

The ordering you seem to be defining on $\mathbb{R}^2$ is $$ (a,x)<(b,y)\qquad\text{for}\qquad (a<b) \text{ or } (a=b \text{ and }x<y) $$ Suppose $f\colon\mathbb{R}^2\to\mathbb{R}$ is an injective order preserving map. Set $$ T_a=\{(a,x):x\in\mathbb{R}\}, \qquad S_a=f(T_a) $$ Thus the image of $f$ is the disjoint union of the sets $S_a$, for $a\in\mathbb{R}$; moreover, $a<b$ implies that $S_a<S_b$, in the sense that $r\in S_a$ and $s\in S_b$ implies $r<s$.

Note that each $S_a$ is bounded; for instance, from $(a-1,0)<(a,x)<(a+1,0)$, we get $$ f(a-1,0)<f(a,x)<f(a+1,0) $$ and so $f(a-1,0)$ is a lower bound for $S_a$, while $f(a+1,0)$ is an upper bound for $S_a$.

Therefore $S_a$ has a greatest lower bound $l_a$ and a least upper bound $u_a$. Note that the sets $S_a$ have neither a minimum nor a maximum, so $S_a\subseteq(l_a,u_a)$.

Can you now find a contradiction?

For other orders on $\mathbb{R}^2$, an injective order preserving map may exist or not. For instance, take a bijection $f\colon\mathbb{R}^2\to\mathbb{R}$ and order $\mathbb{R}^2$ by $$ \mathbf{x}<\mathbf{y} \text{ if and only if } f(\mathbf{x})<f(\mathbf{y}) $$ Then, by definition, $f$ is an order preserving map.

edited Apr 24 '17 at 17:05

answered Apr 24 '17 at 12:50

egreg

238,574

I'm not sure I understand what is $f$, is it sets that are represented by $a$? – shinzou Apr 24 '17 at 13:33
Also, what about the other ordering I made? – shinzou Apr 24 '17 at 13:34
@kuhaku Not clear what you mean by that. – egreg Apr 24 '17 at 13:46
$S_0$ is bounded above (by $f(1,1)$ e.g.) does it have a supremum in $\mathbb{R}$ ? – Henno Brandsma Apr 24 '17 at 16:36
I edited the question with an example about the distance ordering. – shinzou Apr 24 '17 at 16:58
@kuhaku Does that define an order? – egreg Apr 24 '17 at 17:02
The contradiction is there's a bound on a set that has no bounds? And why do the distances not define an order? There are no points in the opposite direction, all the points are around the yellow vector, isn't this an order of radii from (0,0)? – shinzou Apr 24 '17 at 17:08
@kuhaku What's larger between $(1,2)$ and $(2,1)$? And no, the contradiction is not there, but in the fact that every open interval contains a rational number. – egreg Apr 24 '17 at 17:10
They're equal. ${}$ – shinzou Apr 24 '17 at 17:10
@kuhaku Non sequitur. In $\mathbb{R}^2$, $(1,2)\ne(2,1)$. – egreg Apr 24 '17 at 17:11
Must an order distinguish each element? Can't there be some leeway for equality? – shinzou Apr 24 '17 at 17:12
@kuhaku That's called a preorder. But of course, if a set has a preorder that's not an order, there cannot be an order preserving injective map into an ordered set. – egreg Apr 24 '17 at 17:14
I see now, I wasn't looking for a full order but a partial order or preorder. Are there better maps from $\mathbb R^2$ to $\mathbb R$ that achieve this? – shinzou Apr 24 '17 at 17:31
@kuhaku Any order that divides $\mathbb{R}^2$ into “uncountable layers” like the lexicographic order I showed, will produce the same contradiction. – egreg Apr 24 '17 at 17:33
Even for a preorder or partial order? – shinzou Apr 24 '17 at 17:38

Order preserving map $\mathbb R^2 \mapsto \mathbb R$

1 Answers1