3

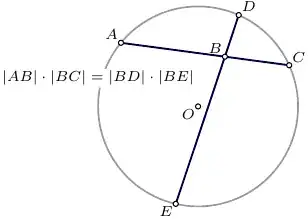
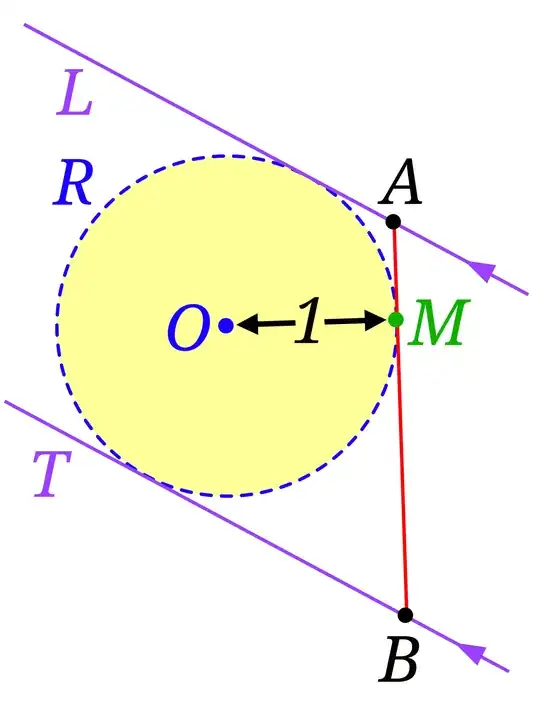
I am trying to prove that the set of all ruler-and-compass constructible points is a subfield of $R$. I have one difficulty though:

  • Given two numbers $\sqrt{a}$ and $\sqrt{b}$ , how can I construct their product and their inverse with rule and compass?
João
  • 63
  • 5
  • How far have you gotten? Where are you stuck? – Ethan Bolker Apr 21 '17 at 19:23
  • Actually I have no idea where to start in the product case. In the inverse case I found out a good idea. – João Apr 21 '17 at 19:43
  • 2
    For product and inverse you also need to know a segment of unit length or how to construct one from the two numbers you have. – g.kov Apr 21 '17 at 19:47
  • @JoãoGabriel It would be helpful if you include all ideas you have thought of in the question. – shardulc Apr 21 '17 at 20:04
  • 1
    For the inverse: https://math.stackexchange.com/questions/1090733/constructing-the-inverse-of-a-number-geometrically And the product: https://math.stackexchange.com/questions/139340/representing-the-multiplication-of-two-numbers-on-the-real-line – Jean-Claude Arbaut Apr 21 '17 at 20:09
  • why do you want to deal with square roots? That's not needed. – Paramanand Singh Apr 22 '17 at 06:10

3 Answers3

2

Think similar triangles. Make a $1, \sqrt a$ right triangle and then a similar one that is $\sqrt b, \sqrt{ab}$

Ross Millikan
  • 374,822
1

One way to construct a product, an inverse and also a square root is to use Intersecting chords theorem:

enter image description here

But we also need to know a segment of unit length.

For example, if $|AB|=a$, $|BC|=b$, and a unit length $|BD|=1$, then $a\,b=|BE|$. But if a unit length is instead $|BE|=1$, then $a\,b=|BD|$.

The same construction can be used to get an inverse of a number as well as a square root.

g.kov
  • 13,581
0

In the next picture it is $AM×BM=1$ enter image description here Proof: The figure formed by the tangent to the unitary circle and the two parallel lines tangent to the unitary circle itself, can be completed to a rhombus whose sides touch the unitary circle, we know that the center of the circle tangent to the sides of a rhombus is the point of intersection of its diagonals and we know that the two diagonals of the rhombus are perpendicular

So $AO⊥BO$.

We know that the tangent to a circle at a point is perpendicular to the radius of the circle that includes the point of tangency

So $OM⊥AB$.

$OM$ is the height of the hypotenuse in a right triangle $∆AOB$, so: $OM^2=AM⋅BM$ $⇒AM×BM=1$

زكريا حسناوي
  • 2,296