Evaluate:
$$ \int_0 ^{+\infty} \frac {x^{a-1} dx} {1+x^3} $$ for $0 < a < 3$.
In the other problems in this section, we try to extend the bounds of the integral to $-\infty, +\infty$ so that it's a closed curve and we can solve for the residues.
However, I don't think we can do that here since it's not an even function.
the "$a$" in the numerator is giving me some problems.
The first thing is that I will evaluate the more general integral
\begin{align*} I_{a,n} = \int_0^{\infty} \frac{x^{a-1}}{1+x^n} \mathrm{d}x = \frac{1}{n} \int_0^\infty \frac{u^{a/n-1}}{1+u}\mathrm{d}u \end{align*} with $u \mapsto x^n$. I actually evaluated the last integral in my soon to be published master thesis about Hankel forms and Dirichlet series.
The last integral is the same as the Mellin transform of $f(x) = 1/(1+x)$ that is \begin{align*} \mathcal{M}_f(s) = \int_0^{\infty} x^{s-1} f(x) \mathrm{d}x = \frac{\pi}{\sin \pi s} \end{align*} We will compute this Mellin transform using complex analysis, and then you can use the first line to obtain the value of your integral. Consider the branch of $z^{s-1}/(z+1)$ defined on the slit plane $C\backslash[0,\infty)$ by
\begin{align*} f(z) = \frac{r^{s-1}e^{i(s-1)\theta} }{z+1}\,, \end{align*}
where $z = re^{i\theta}$, and $\theta \in (0,2\pi)$. For small $\varepsilon$ and $R > 1$, we consider the keyhole domain $C$,
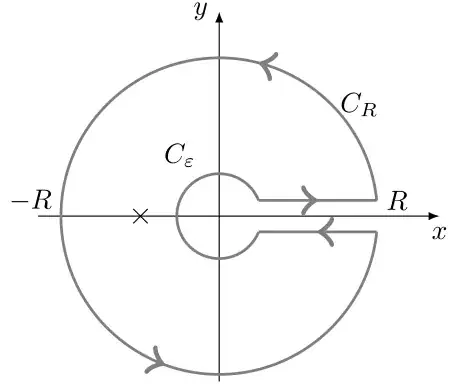
consisting of $z$ in the slit plane $\mathbb{C}\backslash[0,\infty)$ satisfying $\varepsilon < |z| < R$, see the figure above. Since $f$ has a simple pole at $ =-1$, Cauchy's residue theorem yields
\begin{align} \int_C f(z) = 2\pi i \operatorname{Res}\limits_{z = -1}f(z) = -2\pi i e^{\pi i s}\,. \tag{0} \end{align}
The integral over $C$ breaks into the sum of $4$ integrals.
\begin{align} \begin{split} \int_{C} f(z) \mathrm{d}z & = \int_{\varepsilon}^R \frac{x^{s-1}}{x+1} \mathrm{d}x + \int_{C_R} \frac{z^{s-1}}{z+1} \mathrm{d}z \\ & + \int_R^{\varepsilon} \frac{e^{2\pi i(s-1)}x^{s-1}}{1+x} \mathrm{d}x + \int_{C_\varepsilon} \frac{z^{s-1}}{z+1} \mathrm{d}z \,, \end{split} \tag{1} \end{align}
and for the integrals over $C_R$ and $C_\varepsilon$ we obtain the following estimates
\begin{align} \left| \int_{C_R} \frac{z^{s-1}}{z+1} \mathrm{d}z \right| & \leq \frac{R^{s-1}}{R-1} 2\pi R = O(R^{s}) \,, \tag{2} \\ \left| \int_{C_\varepsilon} \frac{z^{s-1}}{z+1} \mathrm{d}z\,. \right| & \leq \frac{\varepsilon^{s-1}}{1 - \varepsilon} 2\pi \varepsilon = O(\varepsilon^s) \tag{3} \end{align}
Letting $R \to \infty$ and $\varepsilon \to 0$ we see that ($2$) and ($3$) vanishes. That is since it is assumed that $0 < s < 1$ in order to assure that the Mellin transform converges. Thus for $\varepsilon \to 0$ and $R \to \infty$ equation ($1$) becomes
\begin{align*} \Bigl( 1 - e^{2\pi i(s-1)}\Bigr)\int_0^{\infty} \frac{x^{s-1}}{x+1} \mathrm{d}x = -2\pi i e^{\pi i s}\,, \end{align*}
where equation ($0$) was also applied. Thus,
\begin{align*} \mathcal{M}_g(s) = \int_0^{\infty} \frac{x^{s-1}}{1+x} \mathrm{d}x = \pi \frac{2i}{e^{\pi i s-2\pi i} - e^{-\pi i s}} = \frac{\pi}{\sin(\pi s)}\,, \end{align*}
and we are done.
It is more practical to use the Laplace transform. For any $a\in(0,3)$ the given integral is convergent and equals (by substituting $x=z^{1/3}$) $$ \frac{1}{3}\int_{0}^{+\infty}z^{\frac{a}{3}}\frac{dz}{z(z+1)}=\frac{1}{3}\Gamma\left(1+\frac{a}{3}\right)\int_{0}^{+\infty}s^{-1-\frac{a}{3}}(1-e^{-s})\,ds =\color{red}{\frac{\pi}{3 \sin\frac{\pi a}{3}}}$$ by the reflection formula for the $\Gamma$ function.
$\newcommand{\bbx}[1]{\,\bbox[8px,border:1px groove navy]{\displaystyle{#1}}\,} \newcommand{\braces}[1]{\left\lbrace\,{#1}\,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\,{#1}\,\right\rbrack} \newcommand{\dd}{\mathrm{d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,\mathrm{e}^{#1}\,} \newcommand{\ic}{\mathrm{i}} \newcommand{\mc}[1]{\mathcal{#1}} \newcommand{\mrm}[1]{\mathrm{#1}} \newcommand{\pars}[1]{\left(\,{#1}\,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\root}[2][]{\,\sqrt[#1]{\,{#2}\,}\,} \newcommand{\totald}[3][]{\frac{\mathrm{d}^{#1} #2}{\mathrm{d} #3^{#1}}} \newcommand{\verts}[1]{\left\vert\,{#1}\,\right\vert}$ \begin{align} \int_{0}^{\infty}{x^{a - 1} \over x^{3} + 1}\,\dd x & = {1 \over 3}\int_{0}^{\infty}{x^{a/3 - 1} \over x + 1}\,\dd x = {1 \over 3}\int_{1}^{\infty}{\pars{x - 1}^{a/3 - 1} \over x}\,\dd x \\[5mm] & = {1 \over 3}\int_{1}^{0}{\pars{1/x - 1}^{a/3 - 1} \over 1/x} \,\pars{-\,{1 \over x^{2}}}\dd x = {1 \over 3}\int_{0}^{1}x^{-a/3}\pars{1 - x}^{a/3 - 1}\,\dd x \\[5mm] & = {1 \over 3}\,{\Gamma\pars{1 - a/3}\Gamma\pars{a/3} \over \Gamma\pars{1}} = {1 \over 3}\,{\pi \over \sin\pars{\pi a/3}} \\[5mm] & = \bbx{\ds{{1 \over 3}\,\pi\csc\pars{{\pi \over 3}\,a}}}\,,\qquad \Re\pars{a} \in \pars{0,3} \end{align}
