How many distinct Unruly boards are there?

Question

Unruly is a puzzle game played on a board of $2n × 2n$ squares. Each square must be colored either black or white, with the following constraints:

• Each column must have $n$ white squares and $n$ black squares.
• Each row must have $n$ white squares and $n$ black squares.
• Nowhere on the board may 3 white squares or 3 black squares appear consecutively, whether horizontally or vertically.

I define two Unruly boards to be equivalent if one can be transformed to the other with any combination of 90° rotations, horizontal flips, vertical flips, or color inversions (i.e., changing all whites to blacks and blacks to whites).

For each $n$, how many non-equivalent Unruly boards are there?

Answer 1

I used a SAT solver to generate all solutions for small values of $n$.

When $n=1$, there's only one solution up to symmetry - just the checkerboard coloring.

When $n=2$, there are $16$ valid $4\times 4$ grids, shown below:

When $n=3$, there are $852$ valid $6\times 6$ grids.

When $n=4$, there are $788,816$ valid $8\times 8$ grids.

The subsequence $(16, 852)$ does not appear in the OEIS except in clearly unrelated entries, so this sequence has likely not been investigated before and isn't equivalent to any particularly nice expression. I would be pretty surprised if there was any kind of closed form.

At $n=5$, iterating over all solutions gets less feasible. If I were to put more time into trying to get a value here, I'd try to use a dynamic programming approach to count boards without symmetry, and then use Burnside's lemma to subtract off all solutions with various additional symmetries (either via more dynamic programming, or using a SAT solver directly on the more restricted solution space).

---

Moving beyond the search for exact values, some very rough thoughts on asymptotics:

A weak upper bound comes from throwing out the three-in-a-row constraint; this gives us A058527 without symmetries (which is only a constant factor of at most $16$), though the sequence there doesn't list asymptotics.

As a lower bound, note that one can tile a $4k\times 4k$ board with either of the following two tiles in each $4\times 4$ subsquare:

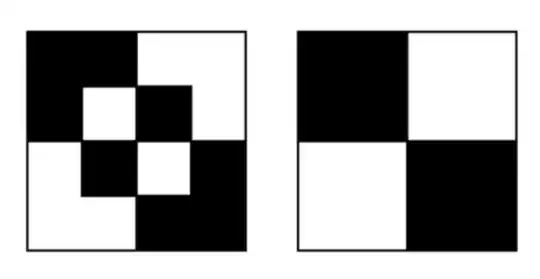
This gives a lower bound of $2^{n^2/4}$, compared to the trivial upper bound of $2^{4n^2}$, so we certainly know that it grows like $\exp(O(n^2))$.

To slightly improve the constants here, we can take the $2415$ $8\times 8$ grids whose borders agree with that of a size-2 checkerboard, such as these ones. This gives us a constant factor of $2415^{n^2/16} \approx 2^{0.702n^2}$; similar strategies on larger boards would converge to whatever the true constant is.

A naive heuristic estimator would suggest, assuming all constraints are independent, that the no-three-in-a-row constraints shrink our possibility space by $(\frac78)^2$ for every interior grid cell, giving a growth rate around $2^{4n^2}\cdot (\frac78)^{8n^2} = 2^{2.459n^2}$. (The sum-to-$n$ constraint is comparatively much weaker at large scales.) Taking into account some second-order effects probably adjusts this slightly—I would guess it causes the heuristic estimate to go up somewhat.