[To check it all out, you may want to visit this interactive page.]
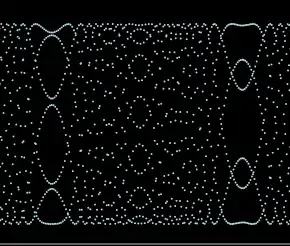
There are several aspects of the plot of $f(x) = \sin(a x^2)$ for integer arguments $x$, that need explanation, especially
its periodicity
the symmetry of the period
its recurring patterns
All these can be explained straight forwardly in a similar way:
Periodicity

$$\sin(a x^2) = \sin(a (c + x)^2) = \sin(a (c^2 + 2cx + x^2)) = \sin(ac^2 + 2acx + a x^2) =\sin(a x^2)$$
if $ac^2 = 2\pi m$ and $ac = \pi$ when $x$ is an integer. With $a = \pi/b$ this is fulfilled for $c = b$, provided $b$ is even. Here, $b=500$.
Symmetry of the period

$$\sin(a x^2) = \sin(a (b - x)^2) = \sin(a (b^2 - 2bx + x^2)) = \sin(ab^2 - 2abx + a x^2) = \sin(a x^2)$$
Recurring patterns
The most prominent recurring pattern is the first peak of $f(x) = \sin(a x^2)$, e.g. for $b = 5000$:



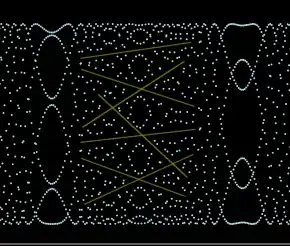
Let's take as an example the third of these patterns which is found exactly in the middle of the period of $f(x) = \sin(a x^2)$, i.e. at $x_0 = b/2$.
Enlarged, it looks like this:
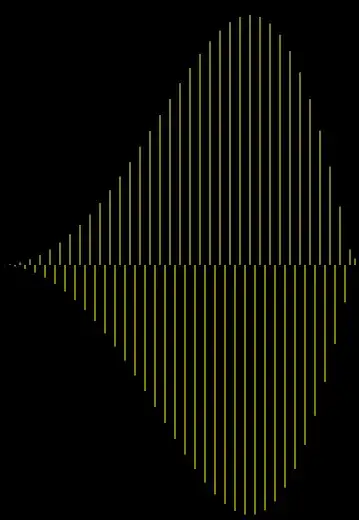
We find:
$$\sin(a (2x)^2) = \sin(a (x_0 + 2x)^2) = \sin(a (x_0^2 + 4x_0x + 4x^2)) = $$
$$\sin(ax_0^2 +4ax_0x + 4ax^2) = \sin(\pi b/4 + 2\pi bx + 4a x^2) = \sin(4a x^2)$$
which holds when $b$ is divisible by $8$. A similar calculation shows that in this case
$$\sin(a (2x+1)^2) = -\sin(a (x_0 + 2x+1)^2)$$
This is still not the whole story to be told, but a beginning.