Calculate the area of a pixel on a sphere

Question

Given an photographical image of a sphere, i.e. an circle with radius $r$ quantized into uniform, square pixels, how can one calculate the equivalent area of the sphere covered by each pixel?

I'm assuming that the projection is parallel.

Example: Let a sphere of radius $R = 1$ be projected to a circle with a radius of $r = 100\,\mathrm{px}$, where the center of the sphere is the center of the middle pixel $(50, 50)$ in the image.

Basically I'm interested in the reverse projection from the pixel space to the sphere.

I guess I have to cast rays from the corners of the pixel onto the sphere and from those four points get the area of the sphere in the section that is encased in the four points.

Answer 1

An area element in spherical coordinates is given by $$\mathrm d A=r^2\sin\phi \mathrm d\phi \mathrm d\theta,$$ following the convention shown here:

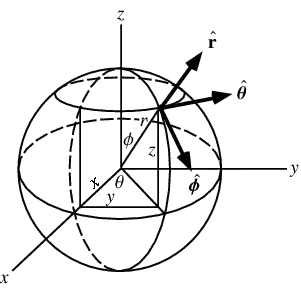
Place your sphere at the origin and say your projection is orthogonal to the $x,y$-plane, i.e. parallel to the $z$-axis. You now have a pixel. Let its bottom-left corner (as seen in the $x,y$-plane) have coordinate $(nd,md)$ with $d$ being the pixel width and $|n|,|m|<\frac{r}{d}$. You now project this pixel onto the sphere and want to know what the corresponding area on the sphere is. To do this, simply integrate the above mentioned area element over the limits in spherical coordinates corresponding to the change in $x$ and $y$, being $x_1=nd\rightarrow x_2=(n+1)d$ and $y_1=md\rightarrow y_2=(m+1)d$ respectively. However, we want to find these limits in terms of $\theta$ and $\phi$, i.e. $\theta_1,\theta_2$ and $\phi_1,\phi_2$, so that we can calculate the projected area of pixel $n,m$ by $$A_{nm}=\int_{\phi_1}^{\phi_2}\int_{\theta_1}^{\theta_2}\mathrm d A.$$ We have that

\begin{align} \theta&=\arctan\left(\frac{y}{x}\right) \\ \phi&=\arccos\left(\frac{z}{r}\right). \end{align}

Now, the $\theta$-part is easy enough, as \begin{align} \theta_1&= \arctan\left(\frac{m}{n}\right)\\ \theta_2&= \arctan\left(\frac{m+1}{n+1}\right). \end{align}

However, the $\phi$-part requires knowledge of $z$, but since we are always only projecting onto the surface of the sphere, we know that $$x^2+y^2+z^2=r^2 \implies z=\sqrt{r^2-x^2-y^2},$$ (note that I've chosen the positive solution... If I were you, I would rotate my coordinate-system each time you're working with pixels lying outside of the first quadrant)

which gives \begin{align} z_1&=r\sqrt{1-\frac{d^2}{r^2}(n^2+m^2)} \\ z_2&=r\sqrt{1-\frac{d^2}{r^2}((n+1)^2+(m+1)^2)}. \end{align} But with this, we can calculate the remaining limits:

\begin{align} \phi_1&=\arccos\left(\sqrt{1-\frac{d^2}{r^2}(n^2+m^2)}\right)\\ \phi_2&=\arccos\left(\sqrt{1-\frac{d^2}{r^2}\left((n+1)^2+(m+1)^2\right)}\right), \end{align}

such that the integral evaluates to

\begin{align} A_{nm}&=r^2(\theta_2-\theta_1)(\cos\phi_1-\cos\phi_2)\\ &= r^2\left(\arctan\left(\frac{m+1}{n+1}\right)-\arctan\left(\frac{m}{n}\right)\right)\left(\sqrt{1-\frac{d^2}{r^2}(n^2+m^2)}-\sqrt{1-\frac{d^2}{r^2}\left((n+1)^2+(m+1)^2\right)}\right) \end{align}

In conclusion, this is a formula for the area of the pixel with $x,y$-coordinates $(nd,md)$ projected onto a sphere that has center at the origin and radius $r.$ Do this for every pixel whose projection is completely on the sphere (the formula does not work otherwise) and you can find your desired ratio.

Doing concrete calculations with this requires care w.r.t. principal values and such, but as I mentioned, I'd strongly recommend rotating your coordinate system when working with the pixels lying in other quadrants of the $x,y$-plane than the first.

Do leave a comment if you have any questions.