17

I apologize for such a simple question. It has been a while since I took math classes.

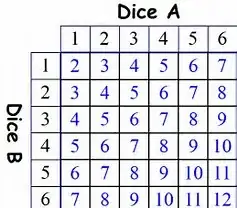
When you roll $2$ dice, there are $36$ possibilities. However, there are only $21$ combinations, if order does not matter. Rolling a $(4,2)$ = rolling a $(2,4)$.

Let's say in a game, rolling a $(1,1)$ makes you lose. The odds of rolling this is a $1/36$. But why can't you say the probability is a $1/21$, assuming you roll both dice at the same time? There's only one combination that makes you lose, so why can't you use $21$ as the denominator?

I have tried searching on this topic, but have not found a good answer. (Most likely because my thinking is fallacious.)

user437992
  • 189
  • 1
  • 5
  • 23
    The problem is that the $21$ cases are not equiprobable. ${1,2}$ is twice as likely as ${1,1}$. – lulu Apr 18 '17 at 16:18
  • 3
    Because to get $(1,1)$, both dice must show a $1$. To get a $1$ and a $2$ it could be either $(1,2)$ or $(2,1)$. – quasi Apr 18 '17 at 16:19
  • 4
    Why do you think that rolling both dies simultaneously is significant? – Aravind Apr 18 '17 at 16:21
  • 1
    lulu, quasi: Both of these comments essentially completely address OP's question. Perhaps one or both of you would consider writing up an answer? – Travis Willse Apr 18 '17 at 16:22
  • 2
    Because order matters in determining how frequently/probable each combination happens. Suppose the dice are named Harry and Bob. They were named by invisible die fairies the no human beings can see or know about. We can't tell Bob an Harry apart. But in their dice souls Bob and Harry can. Rolling a {1,2} can happen if Harry is a 1 and Bob is a 2. Or if Bob is a 1 and Harry is a 2. That' 2 ways so it is twice as probable as both Bob and Harry being both. Even though we mere mortals can not tell the difference between the two. – fleablood Apr 18 '17 at 16:25
  • "Why do you think that rolling both dies simultaneously is significant?" I think because then we can not tell the difference between (1,2) and (2,1). If the dice are indistinguishable the two cases can't be different. They aren't (1,2) or (2,1); they are simply {1,2} (one of 21 possibilities). Which is why I brought in the dice fairies. But I suppose another way of putting it, by making the dice indistinguishable, means that {1,2} is twice as frequent as {1,1}. – fleablood Apr 18 '17 at 16:28
  • 1
    Just because buying a lottery ticket has only 2 outcomes (either you win or you lose) doesn't mean you have a 1/2 chance to win and 1/2 chance to lose. – Seth Wyma Apr 18 '17 at 22:05

6 Answers6

25

The key point is that if you distinguish the two dice all $36$ possibilities are equally likely. That is the only thing that allows you to convert number of possibilities to probability.

If you don't distinguish the two dice then there are only $21$ possibilities, but some of them are more likely than others -- and this issue gets more complicated the more dice you have. So knowing that there are $21$ possibilities doesn't give you a probability of $1/21$.

To extend your approach to a point where it more clearly doesn't work, suppose I change all the numbers other than $1$ to $2$s (so each die has $1,2,2,2,2,2$ on it). This clearly doesn't affect the probability of double-$1$, but now there are only three possibilities...

Especially Lime
  • 40,828
  • 3
    This seems to get closest the asker's misunderstanding. In many cases, when there are finitely many options, we think of all options as equally likely: if you say "I roll a die" you think each of {1, 2, 3, 4, 5, 6} is equally likely; if you say, "I toss a coin", you think of heads and tails as equally likely; if you say, "I draw a card", you think any card has equal probability to come up. However, this is really an unusual and particular feature of those examples. "Throwing two distinguishable dice" (with 36 outcomes) is another; but "throwing two indistinguishable dice" (21 outcomes) is not. – Mees de Vries Apr 18 '17 at 17:39
17

Paint the dice different colors, say red and blue. Now (red 1, blue 2) is clearly different from (red 2, blue 1). But the dice don't know they're painted, because they're dice.

Michael Lugo
  • 22,354
8

In order to throw (1, 1), the values of both dice (let's call them A and B) need to equal 1. Since these events are statistically independent of one another:

$$Prob[(1, 1)] = Prob[A = 1\,and\,B = 1] = Prob[A=1] Prob[B=1] = \frac{1}{6} \cdot \frac{1}{6} = \frac{1}{36}$$

If you specify that $(1, 2) = (2, 1)$, it essentially does not make a difference whether $A=1$ and $B=2$, or $A=2$ and $B=1$. In this case, the probability of throwing (1, 2) comes down to:

$$Prob[(1, 2)] = Prob[A = 1\,and\,B = 2] + Prob[A = 2\,and\,B = 1] = \frac{1}{36} + \frac{1}{36} = \frac{2}{36}$$

As you can see, the events $(1, 1)$ and $(1, 2)$ are not equiprobable: the former has a probability of 1/36, while the latter has a probability of 1/18.

There are six types of throws with equal numbers $(1, 1), (2, 2), \ldots, (6, 6)$ and fifteen types of throws with different numbers $(1, 2), (1, 3), \ldots, (5, 6)$. Since these events cover the total sample space, the sum of the probabilities equals:

$$6 \cdot \frac{1}{36} + 15 \cdot \frac{2}{36} = \frac{36}{36} = 1$$

jvdhooft
  • 7,589
  • 9
  • 25
  • 47
7

Because to get $(1,1)$, both dice must show a $1$. To get a $1$ and a $2$, it could be either $(1,2)$ or $(2,1)$.

Here's another way to look at it ...

The probability of getting $(1,1)$ is $$\frac{1}{6}\times\frac{1}{6} = \frac{1}{36}$$ Explanation: The dice are independent and each die has probability $\large{\frac{1}{6}}$ of showing a $1$.

To get a $1$ and a $2$, the first die must show either $1$ or $2$, and the second die must show whichever of $1,2$ did not show on the first die. Hence the probability of getting a $1$ and a $2$ is $$\frac{2}{6}\times\frac{1}{6} = \frac{2}{36}$$

quasi
  • 58,772
6

Simply because, no matter what, you have 36 possibilities! $6*6 \qquad possibilities = 36$

enter image description here

Well, this makes it even more obvious compared to other explanations, and you can see that combinations occur once or more. But there are only 21 combinations: $[1,1],[2,2],[3,3],[4,4],[5,5],[6,6],[1,2],[1,3],[1,4],[1,5],[1,6],[2,3],[2,4],[2,5],[2,6],[3,4],[3,5],[3,6],[4,5],[4,6],[5,6]$. So you are right about there being 21 combinations. But, you also have $[3,1], [3,2]$ etc. Therefore, because $[a,b]=[b,a]$, the possibilities for $[a,b]$, where $ a \neq b$ is $\frac{2}{36} = \frac{1}{18}$ You have 6 doubles, and 15 combinations, leading to $2*15 + 1*6 = 36$ combinations! (Where in $[a,b]$, $a \neq b$, will count as 2 combinations!

I know that it is a bit repetitive ,so if you think anything is missing, please comment below!

Xetrov
  • 2,089
4

The main problem is that the answer of $\frac1{21}$ doesn't fit with empirical data, and so must be wrong.

Throw the dice $1,000,000$ times and count the number of occurrences of $(1,1)$. It will be around $27,778$ (from $\frac1{36}$), whereas if the probability was $\frac1{21}$ we would expect an answer around $47,619$.

So we must assume $\frac1{21}$ is the wrong answer, and this is because, whether the dice are identical (shape, size, colour, etc..) or not, there are still $36$ possibilities.

JMP
  • 21,771