Limit of uniformly continuous functions with convergent improper integrals.

Question

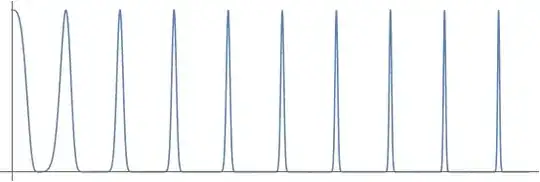
I am struggling with the proof of the following theorem:

Let $f(x)$ be uniformly continuous in $[a, \infty)$ s.t. the integral $\int_a^{\infty} f(x)dx$ converges. prove that $\lim_{x \to \infty} f(x) = 0$.

I came to the conclusion that it is enough to prove that $\lim_{x \to \infty} f(x)$ exists, and from there I have a proof that the limit is $0$.

I tried to use Cauchy's equivalent definition for the convergence of the improper integral + his definition for a regular limit at $x \to \infty$ with no success...

I will be happy to get hints as for how I should proceed, not proofs, since I really want to crack this one by myself, only I spent a pretty long time with no success.

Thank you :)

Answer 1

Let $\varepsilon >0$ given. There exists a $\delta>0$ such that if $x,y \geq a$ are such that $|x-y|<\delta$, then $|f(x)-f(y)|<\varepsilon$. Let $F(x)=\int_a^x f(t)dt$. Then $F(n\delta)$ has a limit, and hence there exists an $N$ such that $|F((n+1)\delta)-F(n\delta)|<\delta \varepsilon$ for $n\geq N$.

There exist a $c_n\in (n\delta, (n+1)\delta)$ such that $F((n+1)\delta)-F(n\delta)=\delta f(c_n)$ (Why ?). What can you say about $|f(c_n)|$ for $n\geq N$ ? And of $|f(x)|$ for $x> A=N\delta$ ?

Answer 2

Hint. If $\lim_{x\to\infty} f(x)$ fails to exist but the integral $\int_{a}^{\infty} f(x) \, dx$ converges, then we often observe a 'train of narrowing peaks':

$\hspace{3em}$

This means that you begin to see an abrupt change in $f(x)$ for large $x$. How the uniform continuity enters this picture is that it prevents peaks from being both high and narrow. So it becomes harder to observe high peaks as $x\to\infty$.

Sketch of Proof. (Hover the cursor to see the content.)

To convert this argument to a solid proof, assume otherwise that $|f(x)| \nrightarrow 0 $. Then you can find $\epsilon > 0$ and $x_n \to \infty$ such that $|f(x_n)| > \epsilon$. Now you can utilize uniform continuity to argue that there exists $\delta, \epsilon > 0$ for which $$ \left| \int_{x_n-\eta}^{x_n+\eta} f(t) \, dt \right| \geq \delta $$ holds for all $n$. (I will leave this part to OP.) This shows that $\int_{a}^{x} f(t) \, dt$ is not Cauchy as $x \to \infty$, so it cannot converge as $x \to \infty$.

Answer 3

Hint: The requirement of uniform continuity is precisely there so that you don't have to worry about the existence of a limit. The following statement is true as well:

Let $ f : [a, \infty) \to \mathbb R $ be a continuous map such that $ \lim_{x \to \infty} f(x) = L \neq 0 $ exists. Then, the integral

$$ \int_a^{\infty} f(x)\, dx $$

diverges.

Try to think of an example where your weaker statement fails with a continuous function that is not uniformly continuous. How does uniform continuity remedy the problem?