How to draw $(g \circ f)$ is surjective, $f$ is not surjective

Question

I'm writing a proof wherein for one part I'm supposed to prove or disprove:

Let $f: X \to Y$ and $g: Y \to Z$ be two functions, with $X = Y = Z = \mathbb{R}$.
If $f$ is surjective, then $(g \circ f)$ is surjective.

[The domains and codomains of $f(x)$ and $g(f(x))$, respectively, are the real numbers.]

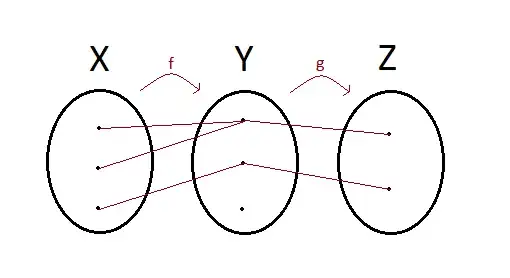
I've already seen a proof by elements showing that this statement is false. However, I want to do a proof by drawing the sets and showing a counterexample where $(g \circ f)$ is surjective but $f$ is not.

We didn't really go over in detail how to do these set drawings, so I think that I figured out a counterexample that disproves the statement, but I'm not confident that I drew it correctly.

I'd really appreciate if someone could let me know if this is logically sound or if I broke a rule I didn't know about, and if so, how I might go about fixing it. Thank you!

I used you guys' answers from the last question to understand how to make the (g o f) drawing surjective. I thought it meant it was surjective from Y->Z instead of from X->Z. But no one really answered in a way that gave me an "aha" moment, so I simplified it a bunch and figured out an example that I actually thought was right, and asked again — BabaSvoloch, Apr 17 '17 at 01:38
What is your question? Whether that diagram is right? Then yes it is right. — DHMO, Apr 17 '17 at 01:39
Thanks. I got some feedback last time but wasn't sure that I understood it correctly. Do you recommend I delete this post? I apologize if I shouldn't have listed it — BabaSvoloch, Apr 17 '17 at 01:41
Your $g$ is not a function in your picture.The lowest point has no value. — Henno Brandsma, Apr 17 '17 at 08:46

score 1 · Answer 1 · answered Apr 17 '17 at 08:45

1

Your picture is in itself correct, except that $g$ needs to be a full function.

But why not make it formal:

$X= \{1,2,3\}, Y = \{1,2,3\} ,Z = \{1,2\}$ and define

$$f: X \rightarrow Y\text{ by }f(1) = f(2) = 1, f(3) = 2$$

And

$$g: Y \rightarrow Z\text{ by }g(1) =1, g(2)=2,g(3)=2 $$

Then $f$ is not surjective as $3 \in Y$ is not an image of $f$, while

$$(g \circ f)(1) = g(f(1)) = g(1) = 1, (g \circ f)(2) = g(f(2)) = g(1) = 1, (g \circ f)(3) = g(f(3)) = g(2) = 2$$

Which shows that $g \circ f$ is surjective, as $1$ and $2$ are image points.

answered Apr 17 '17 at 08:45

Henno Brandsma

242,131

The problem is that the question (now) insists that all the sets are $\mathbb{R}$; which I don't think is helping him understand what the issues are. – ancient mathematician Apr 17 '17 at 09:51
@ancientmathematician thanks for pointing it out. It's a weird requirement indeed. – Henno Brandsma Apr 17 '17 at 10:26

score 1 · Answer 2 · answered Apr 17 '17 at 09:58

I just offer this as an example to think (hard) about.

Let $X=\{0\}$, $Y=\{0,1\}$, $Z=\{0\}$.

Let $f:X\to Y$ be such that $f:0\mapsto 0$.

Let $g:Y\to Z$ be such that $g:0\mapsto 0$, $g:1\mapsto 0$.

Then $g\circ f:X\to Z$ is such that $g\circ f:0\mapsto 0$.

Now $g\circ f$ is clearly surjective, but $f$ is not; although of course $g$ is.

Also $g\circ f$ is clearly injective, but $g$ is not; although of course $f$ is.

Once you (really ) understand this example you can adapt it to suit most prescriptions on the sets.

How to draw $(g \circ f)$ is surjective, $f$ is not surjective

2 Answers2