The most effective windshield-wiper setup. (Packing a square with sectors)

Question

I was on the bus on the way to uni this morning and it was raining quite heavily. I was sitting right up near the front where I could see the window wipers doing their thing. It made me think "what is the best configuration of window wipers for cleaning the maximum area of window?"

Rather than dealing with rectangles of arbitrary size, it is good to start by looking at the specific case of a square.

To abstract the problem into a mathematical format, I'll restructure it like so:

What is the maximum proportion of a square that can be packed with non-overlapping circle-sectors with origins on the edge of a square?

However, $($while still sitting on the bus$)$ I realised that the answer is always "the whole square". This is because you can recursively define configurations of sectors that get closer to each other with a smaller angle, as shown below:

The way to get around this "solution" is by adding another restriction: The sectors should be uniquely defined by their origin and radius. This is possible if "every sector must have the maximum angle possible where the radius doesn't leave the square". For example, even the first case for the sequence I gave is no longer allowed. The two sectors have angles of $\frac{\pi}{4}$, but with the new rule the arcs must both have angles of $\frac{\pi}{2}$ as their radii stay in the square for this angle. However, in this case the two sectors overlap, showing that it is an illegal configuration. Here are some examples of allowed configurations:

Clearly various "infinite" things happen, as these all resemble apollonian gaskets. It seems like a calculus problem but I've spent too much time dealing with topology that I'm not really sure where to start!

Once the square case is covered, it's natural to generalise to rectangles and parallelograms, and eventually to any polygon. Once all polygons are "solved", any two dimensional shape bounded by a closed curve may be solvable as well! Any thoughts and discussion will be appreciated.

EDIT A number of people (mainly friends making fun of me at uni) have pointed out that real windshield wipers do overlap, and that's fundamental to their effectiveness. I realise this, but for the purpose of mathematical abstraction I felt that "supposing there is no overlap" creates an ideal level of complexity.

Some more precision Let $P$ be a polygon with boundary $\partial P$. (First suppose $P$ is a square, but it will definitely be interesting to generalise.) Let $o_i$ be points in $\partial P$, and $r_i \in \mathbb{R}$. Then each pair $o_i, r_i$ uniquely determines a circle $C_i$ centred at $o_i$. Label each of the points where $C_i$ intersects $\partial P$, and draw straight lines from these points to $o_i$. This splits the circle into sectors. Now remove every sector that encloses a point outside of $P$. The sector(s) you are left with depend only on the starting point, radius, and polygon. Given that you can have as many starting points as needed, what is the greatest proportion of the polygon (in terms of area) that can be packed by these sectors which do not overlap?

Suggested variations

1. What is the optimal solution where you try to maximise the area which is cleaned but minimise the number of wipers?
2. It seems like the 4th diagram is probably the solution to the square. But what if only finitely many wipers can be used? What is the solution for each $n$?
3. What if you do in fact let the sectors overlap? (This will completely change the nature of the problem as it isn't meaningful unless the dynamics of the wipers is considered.)

Answer 1

You have made the assumption that all windscreen wipers require a pivot therefore over complicating things. An optimal solution would be that of two windscreen wipers with the height of the window translating instead of rotating from the middle to the two sides. But say you still want there to be pivots. A smart idea could be three wind screen wipers like below (you must have alternating wiping for overlaps). Blue for circumference covered and red for the wipers.

Your 4th diagram does seem optimal but How would the driver see?

Answer 2

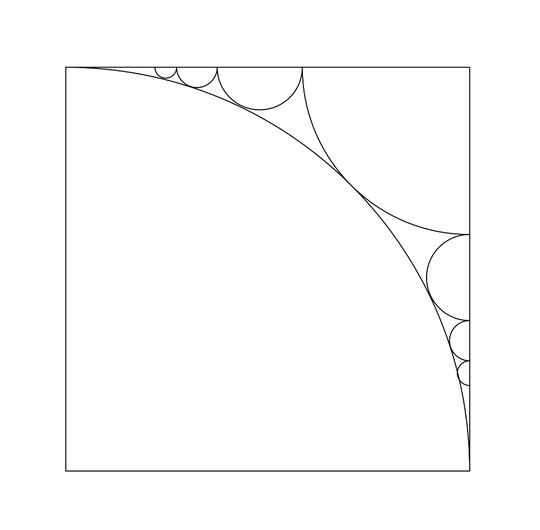
Very interesting question indeed! So for now the goal is to prove your fourth diagram to be optimal. I am most likely not going to be able to prove this by myself, but I have some observations that I strongly believe to be useful in a proof. I also have some conceptual ideas to continue the proof and maybe even finish it, so my main goal is to inspire other people to continue or even finish the proof.

Proposition 1: Consider the area under a monotone increasing curve $f:[0,1]\to[0,\infty)$, so the set $$S:=\{(x,y):0\leq x\leq 1,0\leq y\leq f(x)\}.$$ Consider placing at most $n$ upper-semicircles with their centers on the $x$-axis. Then there is a configuration of largest area and one can be found by repeatedly placing the largest possible semicircle on the right.

Proof of Proposition 1: First note that the space of possible configurations can be modeled as a compact subset of $\mathbb{R}^{2n}$ by considering the centers and radii as parameters. Then the corresponding area is a continuous function, so it attains a maximum.

Consider a configuration of largest area. Number the semicircles $1$ to $n$ from right to left. Note that we can assume without loss of generality that the semicircles are then ordered from long to short. If not, we can simply keep swapping them until they are, because $f$ is monotone increasing.

Assume for the contrary there exists a semicircle that is not as large as possible. Let $i$ be minimal such that semicircle $i$ is not as large as possible. If $i=n$ we immediately get a contradiction. Let $r$ and $s$ be the radii of semicircles $i$ and $i+1$. We can increase $r$ and decrease $s$ by some $\varepsilon>0$. Because $r\geq s$ this gives a configuration of larger area, so again we have a contradiction. $\square$

Corollary 2: If infinitely many semicircles are allowed, there is still a configuration of largest area and one can be found by the same procedure.

Corollary 3: In the case $f(x)=hx$ the largest possible area with infinitely many semicircles is $$\frac{\pi h}{8\sqrt{h^2+1}}.$$ Actually finding this formula is just a lot of algebra, but feel free to verify.

The next logical step would be to consider the case where we have a right angled triangle and we can only place window wipers with their pivot on one of the legs and radius at most the distance to the hypotenuse. This becomes more difficult, not only because the window wipers on different legs influence each other, but also because not all wiping areas have to be semicircles anymore. From here on, let me just lay out some ideas to continue or even finish the proof.

First, let me note that I suspect this triangle case to be optimally solved by placing a quarter circle in the corner, but only if the width and height are within some margin of each other. For the general case, I suspect we want to split into two cases. With or without non-semicircular wiping areas.

First consider the case with non-semicircular wiping areas. Consider the largest non-semicircular wiping area. The rest of the triangle is then split into three regions. Two of them can be at least approximated by the case of Corollary 3 and the final region is again the case we are now trying to solve. Since we are only trying to show a specific configuration is optimal, my idea was to somehow bound the total area of the arbitrary configuration in question using these ideas.

Then for the case without non-semicircular wiping areas. I highly suspect this to never be optimal. For example, if we can place a quarter circle in the corner that does not cut any of the semicircles, then placing this instead of all the semicircles now inside it is obviously a large improvement. However I am having trouble generalizing this argument.

I want to finish off by noting that the conjectured optimal solution has an area of $$\frac{\pi}{2}\left(2-\sqrt{2}+8\sum_{n=1}^\infty\frac{1}{(\sqrt2+2n)^2(\sqrt2+2+2n)^2}\right)\approx0.9697926466...$$ in a unit square. More generally, the largest possible area in Proposition 1 for the function $f:[0,w]\to[0,\infty)$ given by $f(x)=1-\sqrt{1-x^2}$ is $$\frac{\pi}{8}\sum_{n=1}^\infty\frac{1}{\left(n+\frac1w-1\right)^2\left(n+\frac1w\right)^2}$$ if $0<w\leq1$ defines up to where you can place the semicircles.

EDIT: I have some more progress. Mainly the following proposition.

Proposition 4: Consider the area under a curve $f:[0,1]\to[0,\infty)$ with $f(0)=f(1)=0$, which is piecewise convex on $[0,a]$ and $[a,1]$ for some $0<a<1$. Consider placing infinitely many upper-semicircles with their centers on the $x$-axis. Then there is a configuration of largest area and one can be found by repeatedly placing the largest possible semicircle.

Idea of proof of Proposition 4: Like in Proposition 1, for any finite set of semicircles, we can rearrange them so they all touch. In this case, we find there is a largest semicircle, and going to the left or right we find the semicircles will decrease in size. Furthermore, we can assume all semicircles touch the curve $f$.

In the infinite case, we find all semicircles touch each other and the curve of $f$. It follows that the entire set is determined by any specific semicircle, or even any specific semicircle center. This gives a function $A:[0,1]\to[0,\infty)$ which, given any possible semicircle center, outputs the total area induced by that center.

Due to piecewise convexity, there is a unique possible semicircle touching both pieces of the curve of $f$. Let $...,c_{-1},c_0,c_1,...$ denote the induced centers of all the semicircles. We find $A(c_i)$ is independent of $i$. Furthermore, the piecewise convexity of $f$ can be used to show $A$ is convex in any interval $[c_i,c_{i+1}]$, as the sum of two convex functions. It follows that $A$ is maximal at the values $c_i$. $\square$

Remark: Note that $f$ does not need to be continuous at $a$.

We can use this proposition to analyze the following case.

So we have to fill a right angled triangle where all centers have to be on the legs. We consider the case where there is a non-semicircular sector (Purple) touching the hypotenuse. This splits the triangle into three regions: To the left of Purple, above Purple, and the Green triangle. By Proposition 4, it is optimal to place the Blue semicircle touching the hypotenuse and the Purple circular arc. Then all the orange semicircles both on the left of Purple and above Purple follow. The Green region is again a right angled triangle, which makes this problem recursive.

If we let $\varepsilon$ be the width of the Green triangle, we find the total area is a function of $\varepsilon$. Assuming the main triangle has base $1$ and height $h$, the area for $\varepsilon=0$ can be calculated as $$A_0(h)=\frac\pi{4}r^2+(1-r)^2f(h)+(h-r)^2f\left(\frac1h\right),$$ where $r=h/\sqrt{h^2+1}$ is the radius of the Purple circular arc, and $f(h)=(\pi/8)\cdot h/\sqrt{h^2+1}$ is the area found in Corollary 3. Note that the proportional area $A_0(h)/(h/2)\to\pi/4$ both as $h\to0$ and as $h\to\infty$. For $h\in(0,\infty)$, the proportion is larger, taking a maximum of $(3\sqrt2-2)\cdot(\pi/8)$ at $h=1$.

It can be argued for small values of $h$ that the difference between $A_0(h)$ and the optimal area is $O(h^2)$. So we know approximately how well the Green triangle can get filled. For $\varepsilon>0$ we find a total area of $$A_\varepsilon(h)=A_0(h)+\varepsilon\left[\left(\frac12+\frac\pi{8}\right)r+2h(h-r)f\left(\frac1h\right)-2A_0(h)\right]+O(\varepsilon^2).$$ Note that we still use $r=h/\sqrt{h^2+1}$ rather than the radius of the new Purple circular arc.

This gives the derivative of $\varepsilon\mapsto A_\varepsilon(h)$ at $\varepsilon=0$. With Wolfram Alpha, we find this derivative is negative in approximately the interval $h\in(0.5605,6.6187)$, and positive outside this interval. This proves that taking $\varepsilon=0$ is not always optimal, but it is also evidence that it is optimal for $h$ close to $1$.

Finally, the formula for the area in Proposition 1 for the curve $f:[0,w]\to[0,\infty)$, $f(x):=1-\sqrt{1-x^2}$ can be simplified, kind of, by $$\frac{\pi}{8}\sum_{n=1}^\infty\frac{1}{\left(n+\frac1w-1\right)^2\left(n+\frac1w\right)^2}=\frac\pi{8}\left[2\zeta\left(2,\frac1w\right)-w^2-2w\right],$$ with $\zeta(s,a):=\sum_{n=0}^\infty(n+a)^{-s}$ the Hurwitz zeta function. This makes the conjectured optimal area in a unit square equal to $$\frac\pi{2}\left(2\sqrt2-3+\zeta\left(2,1+\frac12\sqrt2\right)\right)\approx0.9697926466...$$ This should allow one to do an analysis similar to my analysis of the triangle, but with a circular sector as hypotenuse.