2

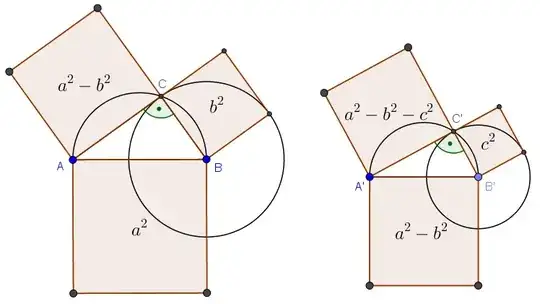
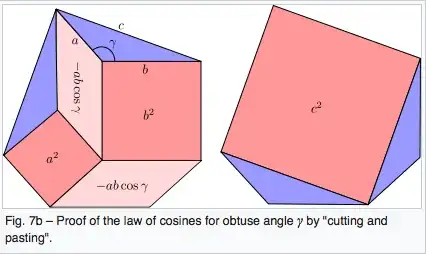
Given are three squares of side lengths $a$, $b$ and $c$ with $a>b>c$. Construct (with compass and straightedge) a square of the area $a^2-b^2-c^2$!

I have thought about "cutting" the two smaller squares into pieces and arranging them inside the big square in such a way that the space left is a square, too.

Do you have any ideas?

mxian
  • 2,019
  • 1
    Do you mean construct with compass and straightedge, or with scissors, or what? – Ross Millikan Apr 11 '17 at 16:31
  • I mean construct with compass and straightedge. The "cutting" that I mentioned was just an idea to develop a strategy. I will edit the question to make this clearer. – mxian Apr 11 '17 at 16:42
  • $a>b>c$ does not ensure that $a^2-b^2-c^2$ is non-negative. What if $(a,b,c)=(8,7,6)$, for instance? – Jack D'Aurizio Apr 11 '17 at 17:58
  • @JackD'Aurizio I noticed that, too but that's how the task is stated. I am quite sure they mean $a>b$ and $a^2-b^2>c^2$. – mxian Apr 11 '17 at 18:21

3 Answers3

1

I have actually found out myself now and it is a lot easier than the answer given below. Start with the square of the area $a^2$. Construct a semicircle towards its outside on one of its edges, say $AB$ and then construct a circle with radius $b$ and with centre $B$. Point $C$ should be the point of intersection of the circle and the semicircle. Then ABC is rectangular and Pythagoras tells us that $$|AC|^2=a^2-b^2.$$ Repeat this process now putting the square of area $a^2-b^2$ on the hypotenuse and the one of area $c$ on one of the legs. Then the square on the other leg has area $a^2-b^2-c^2$, as desired.enter image description here

mxian
  • 2,019
0

We can measure $a$ and $b$ in units of $c$. You can use similar triangles to get segments of length $(\frac ac)^2$ and $(\frac bc)^2$, then can subtract to get $(\frac ac)^2-(\frac bc)^2-1$, then follow this question to get $\sqrt{(\frac ac)^2-(\frac bc)^2-1}$

Community
  • 1
Ross Millikan
  • 374,822
0

Hint:

It is an application of the law of cosines. This figure is from wikipedia, and (changing $c$ and $a$ with respect to your question) shows that $c^2-a^2-b^2=-2ab\cos \gamma$

enter image description here

The two parallelograms of area $-2ab\cos \gamma$ can be transformed in a rectangle of sides $b$ and $d=|2a\cos \gamma|$, and this rectangle can be transformed in a square with a classical construction (that you can find here).

Emilio Novati
  • 62,675