Proving $ \lnot (A \Rightarrow B) \vDash A \land \lnot B $

Question

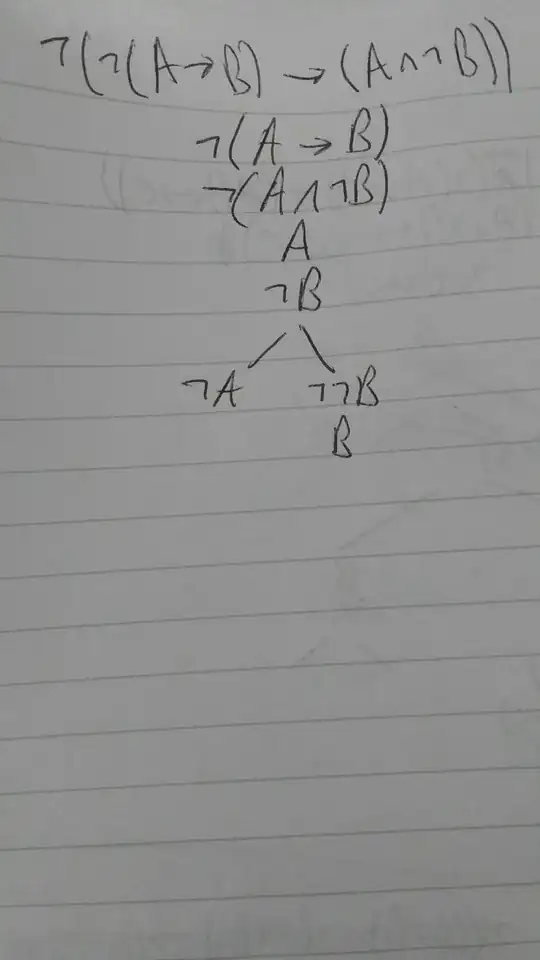
I need help trying to prove $$ \lnot (A \Rightarrow B) \vDash A \land \lnot B $$ in natural deduction.

I've come this far:

$$ \begin{array}{|l}\hline \lnot (A \Rightarrow B) \text{ premise} \\ ~~\begin{array}{|l}\hline B \text{ assumption} \\ ~~\begin{array}{|l}\hline A \text{ assumption} \\ B \text{ copy} \\\hline \end{array}\\ A \Rightarrow B \\ \bot \\\hline \end{array}\\ \lnot B \\ ~~\begin{array}{|l}\hline \lnot A \text{ assumption}\\\vdots\\\hline \end{array}\\\hline \end{array} $$

And then...?

score 6 · Accepted Answer · answered Apr 10 '17 at 12:25

1) $\lnot (A \to B)$ --- premise

2) $\lnot (A \land \lnot B)$ --- assumed [a]

3) $A$ --- assumed [b]

4) $\lnot B$ --- assumed [c]

5) $A \land \lnot B$ --- from 3) and 4) by $\land$-intro

6) $\bot$ --- from 2) and 5)

7) $B$ --- from 4) and 6) by Double Negation-elim, discharging [c]

8) $A \to B$ --- from 3) and 7) by $\to$-intro, discharging [b]

9) $\bot$ --- from 1) and 8)

10) $A \land \lnot B$ --- from 2) and 9) by Double Negation-elim, discharging [a].

This is a neat and straightforward proof. I like it. – Måns Nilsson Apr 10 '17 at 12:43 — Måns Nilsson, Apr 10 '17 at 12:43

score 1 · Answer 2 · answered Apr 10 '17 at 12:35

1

Your proof is so far so good!

So, to continue from:

$$\neg A \text{ Assumption}$$

$$\text{new box}$$

$$A \text{ Assumption}$$

$$\bot \text{ (from A and not A)}$$

$$B \text{ (from contradiction you can infer anything)}$$

$$\text{end box}$$

$$A \rightarrow B$$

$$\bot$$

$$\text{end box}$$

$$\neg \neg A$$

$$A$$

$$A \land \neg B$$

answered Apr 10 '17 at 12:35

Bram28

100,612
6
70
118

So you are allowed to make directly contradicting assumptions after one another? – Måns Nilsson Apr 10 '17 at 12:41
@MånsNilsson Yes, you can assume anything you want ... The key is to assume things that actually help you prove what you want. – Bram28 Apr 10 '17 at 14:34

score 0 · Answer 3 · answered Apr 10 '17 at 12:20

0

If you assume $\neg A$ you should be able to prove that $A\Rightarrow B$. This can be done by deduction theorem, because if you assume $A$ you can prove $B$ by contradiction (and by deduction theorem you get $\neg A\vdash A\Rightarrow B$). Now with the assumption $\neg(A\Rightarrow B)$ you have a contradiction and can conclude that the assumption $\neg A$ was false or that $A$ is proven.

answered Apr 10 '17 at 12:20

skyking

16,654

How do I prove B by contradiction? – Måns Nilsson Apr 10 '17 at 12:37
@MånsNilsson Since you have already $A$ and $\neg A$ in the assumptions you have your contradiction ready. You just have to assume the negation to whatever you want to prove and then by contradiction conclude it. – skyking Apr 10 '17 at 13:20

score -1 · Answer 4 · edited Apr 10 '17 at 12:52

-1

$ \lnot (A \Rightarrow B) \vDash A \land \lnot B $

Remember that we can write $(A \Rightarrow B)$ as $\lnot A \lor B$.

So we have $\lnot(\lnot A \lor B)$, and distributing the $\lnot$, we get $A \land \lnot B$, as wanted.

edited Apr 10 '17 at 12:52

Mauro ALLEGRANZA

94,169

answered Apr 10 '17 at 12:25

K Split X

6,565

Shaun · Answer 5 · 2017-04-10T12:58:38.873

-1

What you have to do is show that $\lnot (\lnot(A\to B)\to(A\land\lnot B))$ is a tautology. But the tableau of its negation is closed:

.

(Each path contains a contradiction.) Hence the result.

edited Apr 10 '17 at 12:58

answered Apr 10 '17 at 12:45

Shaun

44,997

The question asked for natural deduction, not a tableau proof. – hmakholm left over Monica Apr 10 '17 at 15:43

Proving $ \lnot (A \Rightarrow B) \vDash A \land \lnot B $

5 Answers5

Linked