The equation I'm trying to solve is
$$ \frac{d^2}{dx^2}u = - \frac{1}{1+x^2} $$
on the domain $0 < x < 1$, with boundary conditions $u(0) = 0$ and $\frac{du}{dx}(1)=0$.
I got the weak form equation as:
$$\int_0^1 \frac{du}{dx} \frac{d\psi}{dx} \ dx =\int_0^1\left( \frac 1 {1+x^2} \right)(\psi) \, dx$$
I assumed a linear element.My element stiffness matrix is:
$$ k^e_{ij} = \frac{1}{h} \left[ \begin{matrix} 1 & -1 \\ -1 & 1 \end{matrix} \right] $$
and
$$ f_i^e = \left( \begin{matrix} \arctan h - \frac 1 {2h}\ln(1+h^2) \\ \frac 1 {2h} \ln(1+h^2) \end{matrix} \right) $$
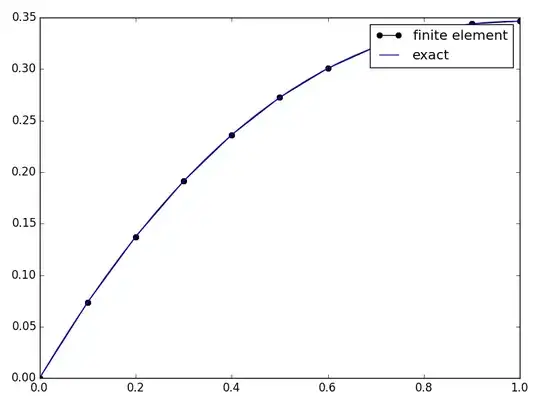
Here are the results for a 10 element model of a python program that I did:
Exact FEM
0.07355 0.09468
0.13721 0.17939
0.19127 0.25413
0.23617 0.31891
0.27245 0.37372
0.30073 0.41856
0.32166 0.45343
0.33587 0.47834
0.34399 0.49329
0.34657 0.49826
Are these results to be expected? Or is there a mistake in the model/matrices above?