If $\alpha$ be a root of
$x^{x-\sqrt{x}} = \sqrt{x}+1$.
We need to find the value(s) of $(\alpha + \frac{1}{\alpha})$. WolframAlpha shows two possible roots of the equation.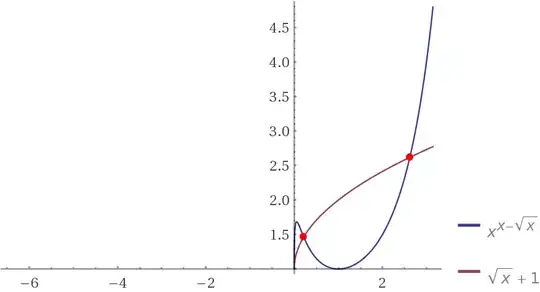
If $\alpha$ be a root of
$x^{x-\sqrt{x}} = \sqrt{x}+1$.
We need to find the value(s) of $(\alpha + \frac{1}{\alpha})$. WolframAlpha shows two possible roots of the equation.
One solution of the equation is:
$x=\frac{3+\sqrt{5}}{2}$.
Therefore
$\alpha+\frac{1}{\alpha}=3$.
Setting $\sqrt{x}+1=t$, the equation can be written as
$t=x^{x-\sqrt{x}}$.
We have an equivalence between two powers.
We know that two powers are equal if they have the same base and the same exponent, so we can assume for a moment that the base $x=t$ and write:
$t=t^{x-\sqrt{x}}$.
This equality of powers implies that since they have the same base ($t$), they must have the same exponent:
$1=x-\sqrt{x}$.
Solving this equation we get
$x=\frac{3+\sqrt{5}}{2}$.
This logic is not working here.
– Aroonalok Sep 07 '21 at 03:47