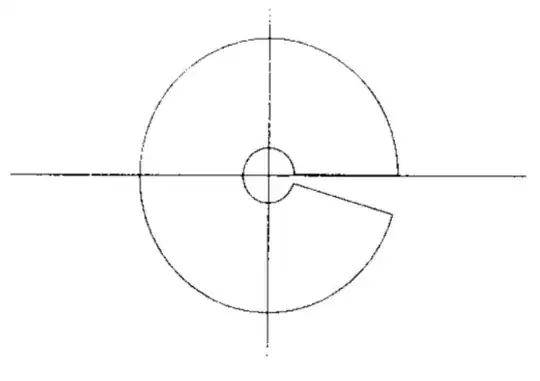
First of all, note that the line that connects the contour to 0 should be horizontal, and the smaller circle closed; the two horizontal lines should coincide. This is called the keyhole countour. Also note that the results holds only for $\alpha \in (0, 1)$
To see why on the inner circle the integral tend to $0$, you should note that while is true that the function blows up to infinity like $z^{-\alpha}$, the radius of the circle is going to $0$ like $z$. Since $\alpha < 1$, the integral vanishes. More formally you can write
$$\left|\int_{|z| = r} \frac{1}{z^\alpha(1+z)}dz \right| \le \int_{|z| = r} \frac{1}{r^\alpha(1-r)} dz = \frac {2\pi r}{r^\alpha(1-r)} \to 0$$ as $r \to 0$.
Now, to compute the integral we write
$$\oint_\gamma \frac{1}{z^\alpha(1+z)}dz = 2\pi i \text{Res}(f(z), -1)$$
Clearly $$\text{Res}(f(z), -1) = \frac 1{(-1)^\alpha} = e^{-i\pi\alpha}$$
So
$$\oint_\gamma \frac{1}{z^\alpha(1+z)}dz = 2\pi i e^{-i\pi\alpha}$$
But since the integral on the big and small circle vanish, all is left is the integral on the two (coinciding) horizontal lines. Since $z^\alpha$ is a multi-valued function, though, on the lower line we need to choose a different branch of the function. Therefore we will write
$$\oint_\gamma \frac{1}{z^\alpha(1+z)} dz = \int_0^\infty \frac{1}{z^\alpha(1+z)} dz - \int_0^\infty \frac{1}{z^\alpha(1+z)e^{2\pi i \alpha}} dz$$
Notice that factor $e^{2\pi i \alpha}$ coming from the different branch of $z^\alpha$ and the minus sign coming from the fact that we travel the two lines in different directions. Therefore
$$\oint_\gamma \frac{1}{z^\alpha(1+z)} dz = \left(1 - \frac 1{e^{2\pi i \alpha}}\right)\int_0^\infty \frac{1}{z^\alpha(1+z)} dz = 2\pi i e^{-i\pi\alpha}$$
Simplifying we finally find
$$\int_0^\infty \frac{1}{z^\alpha(1+z)} dz = \frac {2\pi i e^{i\pi\alpha}}{e^{2i\pi \alpha} - 1} = \frac \pi{\sin(\pi \alpha)}$$