0

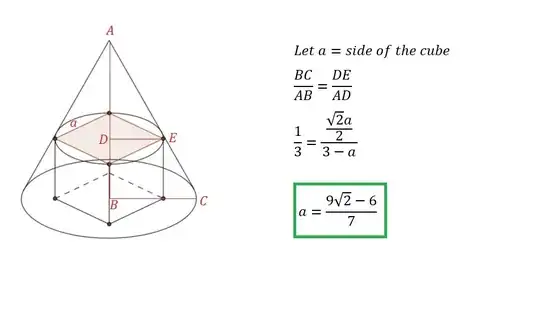
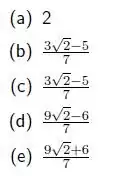A right circular cone has a base of radius $1$ and height $3$. A cube is inscribed in the cone so that one face of the cube is contained in the base of the cone. What is the side-length of the cube?

I tried to make a side projection of this solid: 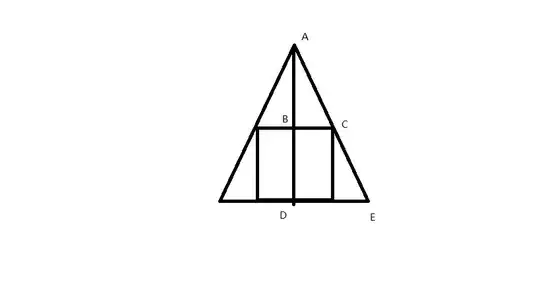enter image description here

$AD=3$ and $DE=1$. $△ABC$ is similar to $△ADE$ and thus $\frac{AB}{AD}=\frac{BC}{DE}$, so the length of the cube is $\frac65$. Unfortunately, there's no such choice. What's wrong with my projection? How should I do this correctly?

Choices: enter image description here

InanimateBeing
  • 3,074
Hank
  • 668
  • I also get with another method (Pythagoras and etc.) $;\cfrac65;$ . Is one of the options $;\cfrac35;$ ? Perhaps they took only one half of the cube? – DonAntonio Apr 02 '17 at 07:48
  • Presumably one of (b) and (c) is meant to have a +5 instead of a -5. – nickgard Apr 02 '17 at 08:47
  • 1
    In your side projection view, the top corners of the cube shouldn't touch the cone at all. If you want the corners to touch the cone, you have to rotate the cube by $45^\circ$, which means the ratio of the (projected) cube's width to its height will be $\sqrt 2$. – TonyK Apr 02 '17 at 11:21
  • I see. I did the wrong projection! Thanks for all of your explanation! – Hank Apr 03 '17 at 02:25
  • is there any problem with the projection which op has drawn – Nebo Alex Feb 18 '18 at 18:01

3 Answers3

6

This is hint rather than a full answer, but it needs a picture.

You have shown the right and left edges of the cube touching the sides of the cone, so let's tilt the whole thing towards you to reveal the orientation of the cube:

Cube inside a cone

nickgard
  • 4,116
3

As pointed out by @NickG, the top face of the cube is inscribed in the circular cross section of the cone. If you let the side length of the cube be $2x$ and the radius of the cross section at the level of the cube's top face be $r$, you get $r = x\sqrt 2$ by the Pythagorean theorem.

If you also let the height of the sub-cone dropped from the vertex to that level (of the top cube face) be $h$, you get $h = H - 2x$.

Now $\frac rh = \frac RH$, so $r = \frac{R(H-2x)}{H}$

Hence $x\sqrt 2 = \frac{R(H-2x)}{H}$ and solving for $x$, we get:

$$x = \frac{RH}{2R + H \sqrt 2}$$

It's now a simple matter to substitute the given quantities and work out the side of the cube (remember that it's $2x$). Don't forget to rationalise the denominator. If you still can't get it to equal one of the choices (you really should), then post a comment.

Deepak
  • 26,801
2

I used the perfect drawing of $Nick G$. enter image description here

Seyed
  • 8,933