Distance between sets with one closed set and one compact set

Question

I would like to prove the following statement.

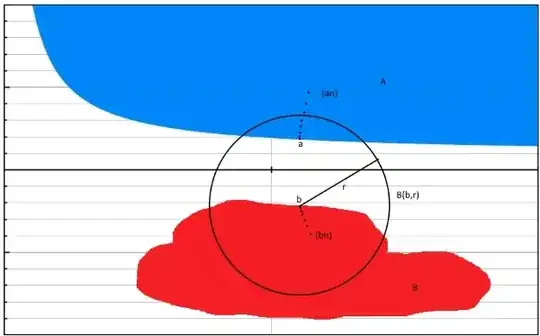
Let A and B be nonempty disjoint subsets of $\mathbb{R}$ where A is closed and B is compact. Then there exists $a \in A$ and $b \in B$ such that $inf${$|a-b|$:$a \in A, b \in B$}=$|a-b|$

A and B disjoint, A compact, and B closed implies there is positive distance between both sets

I read a similar question above where the concept of "limit point" and others were used, but my class (Introduction to Analysis) has not gone that far; most of all, I would like to prove the statement from the knowledge that the class covered.

So far, I have learned definition of limit of a sequence, Bolzano-Weierstrass Theorem. Also, I just learned (and proved) that there exists a sequence ${a_n}$ in E such that $\lim{a_n} = \inf{E}$ if E is a nonempty subset of $\mathbb{R}$ (whether E is bounded below or not due to the extended real numbers).

From the things that I learned, first, I constructed a set $E$={$|a-b|$:$a\in{A}, b\in{B}$} and I know that there exists a sequence ${x_{n}}$ in E such that $\lim{x_{n}}=infE$. Since ${x_{n}} \in{E}, x_{n}=a_{n}-b_{n}$ where $a_{n} \in A, b_{n} \in B$. Let $infE = \beta$. Then, this leads to $\lim{(a_{n}-b_{n})}=\beta$. Then, for any $\epsilon$>0, there exists $N \in$ $\mathbb{N}$ such that $|a_{n}-b_{n}-\beta|<\epsilon$ for all n $\ge$ N.

Then, I could not proceed. I should use conditions that A and B are disjoint, A is closed, and B is compact. Could anyone help me proceed? I had a feeling that using contradiction might work from the link above, but it is quite tough. Since I am a novice (just started taking Introduction to Analysis), I would very much appreciate it if you could help me prove this at the beginner level.

Answer 1

You have your sequences $a_n,b_n$.

• Use compactness of $B$ to obtain a limit point $b$ of $b_n$.
• Show that it is ok to replace $A$ with $A':=A\cap \overline{B_r(b)}$, where $r$ is big enough
• Using that $A$ is closed, show that $A'$ is compact, so that as in the first bullet point we find a limit point $a\in A'\subseteq A$
• Show $\inf E=|a-b|$. From disjointness, this is $>0$.

Answer 2

I wanted to make a comment but it ended up too long ;-)

So I finally write it as an answer, but this is really a discussion about the theorem conditions and graphical support for @Hagen's proof.

As stated by the thread you linked, $A,B$ closed is not a sufficient condition to proove your claim.

This is because the infimum distance may be realized only at infinity.

The counter example given by @gary can be adjusted for a non-zero distance:

It is easier to understand in $\mathbb R^2$

For instance take $A=\{ (x,y)\mid x\ge 0,y\ge 1+1/x\}$ [in blue]

and for $B$ its symetric with respect to axis $x$, i.e. $B=\{(x,y)\mid x\ge 0,y\le-1-1/x\}$. [in red]

They are respectively "asymptotic" to $y=1$ and $y=-1$ thus $d(A,B)=2$ but it is never reached within bounded area: you get $a_n\to(+\infty,1)$ and $b_n\to(+\infty,-1)$

So you have to use the condition that $B$ is also compact (or bounded which is equivalent in $\mathbb R^2$) so you can prevent the adjacent sequences $a_n,\ b_n$ to escape to infinity.

The proof by @Hagen von Eitzen shows the details.

From the convergent subsequence $b_{\sigma(n)}\to b$ in $B$ compact, we can work locally in the disk of center $b$ and radius $r$ (large enough so it intersects $A$ but more importantly contains the convergent part of $(a_n)$), and this is in fact the toughest part of the proof, to show that we can prooceed like that.

This disk has notation $B(b,r)=\{x\mid |x-b|<r\}$ or $B_r(b)$ (B is initial for ball, b is center, r is radius), it is an open set. Since we need $A'$ closed, we have to take $\overline{B(b,r)}$ which mean the closure of this ball, i.e $\{x\mid |x-r|\le r\}$, also called the closed ball of center $b$ and radius $r$.

Thus $A'$ is intersection of two closed sets, so is closed, and also bounded, thus compact.

---

Note that I presented pictures for $\mathbb R^2$ because it is easier to understand, but it works also for $\mathbb R$ yet the counter-example with only two closed sets is less straightforward.

We can take $A=\{10n\mid n\in\mathbb N\}=\{0,10,20,30,...\}$

$B=\{10n+2+1/n\mid n\in\mathbb N^*\}=\{13,22+\frac 12,32+\frac 13+,...\}$

Both are discrete sets, so they are closed but neither is compact, and the infimum distance which is $2$ is realized at infinity.

You can replace the points by small intervals, it suffice they are at least $2+\frac 1n$ apart.

For instance $A=\bigcup\limits_{n=0}^{\infty}[10n,10n+3]$ and $B=\bigcup\limits_{n=1}^{\infty}[10n+5+\frac 1n,10n+7]$