9

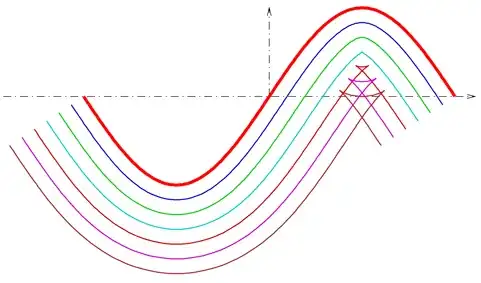
When you compute offset curves (also called parallel curves), by offsetting a fixed distance along the normals to a given curve, the resulting curve self-intersects when the offset distance exceeds the radius of curvature (see below).

I am looking for a practical way to detect and remove the inner "pockets" that appear. The output should be a continuous curve with the self-intersection replaced by a corner point.

My curves are actually cubic arcs, but I work with flattening and discrete points, so one can see the curve as a smooth polyline. In a variant of the question, the offset is also varying along the curve.

enter image description here

Update:

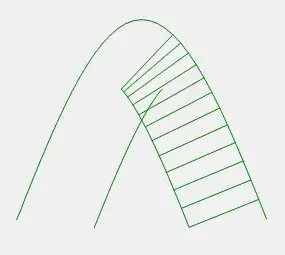
There is a straightforward way to detect the cusps: they arise where the radius of curvature equals the offset distance. In the discrete setting, the osculating circle can be approximated by the circumscribing circle of three consecutive vertices.

In the figure, you see offset vertices, which are in red when the estimated curvature is smaller than the offset. This principle allows to find evidence of self-intersections.

enter image description here

I suspect that the "ladder" formed by the initial polyline and the corresponding offsetted points can help find the intersection efficiently.

enter image description here

  • Possible duplicate of http://math.stackexchange.com/questions/302076/offseting-a-bezier-curve. See the papers by Farouki mentioned in http://math.stackexchange.com/a/302101/589. – lhf Mar 30 '17 at 00:32
  • Nice observation re radius of curvature & offset distance. – Joseph O'Rourke Mar 30 '17 at 12:24

1 Answers1

4

Since your curves are polygonal curves, the offset curves are also polygonal curves. For any given offset curve, you need to detect self-intersection, and then clip off the loop at the self-intersection point. You will need robust code for segment-segment intersection. Then you need to decide on how much you care about efficiency, and how complex an algorithm you are willing to code.

Self-intersection can be tested efficiently by a sweep-line algorithm, but that may be overkill here because the loops tend to be small, so intersections are likely to be local. You could find example algorithms by searching for "polygon self-intersection detection." For example: "Check if Polygon is Self-Intersecting."

Community
  • 1
Joseph O'Rourke
  • 30,327
  • Hi Joseph. Indeed I can use the machinery of sweepline poygon processing. That would both solve the problem of local and global self-intersections. But I am after something simpler, that only needs to work for local self-intersections, preferably with O(1) storage. [I don't mean I have such a stringent memory constraint, I mean truly local computation.] –  Mar 30 '17 at 07:20
  • 1
    Contrary to my initial thinking, you need to backtrack a certain number of steps from the cusps to find the intersection, so that the problem is not purely local. Now, the discretized curve and the offsetted one form a "ladder" which seems to define a (quasi-)regular tiling. I was wondering how to exploit this arrangement to quickly find the intersection. (There is a new picture.) –  Mar 30 '17 at 12:48