Use the method of characteristics to solve $$u_t+uu_x+\frac{1}{2}u=0, \quad t>0, \quad {-\infty}<x<\infty$$ $$u(x,0)=\sin(x)\quad {-\infty}<x<\infty$$ (solution may be expressed in implicit form). Show that a shock solution is possible if $t=t_c=2\ln(2)$.
Notes: Although I have used the method of characteristics to solve the wave equation and have cover basic theory in class. But, I am bit lost in application. Any hints would be appreciated.
Characteristic lines are paths that carry information. If two characteristics collide, there will be two contradictory accounts of the solution there, and the continuum description will break down. At that point, usually $\partial_xu$ becomes infinite.
From the solution given, we know that along a characteristic $$\frac{dx}{dt}=u,\qquad\frac{du}{dt}=-\frac{u}{2}$$ so that the location of the characteristic originating at $x_0$ is $$x=x_0+2u_0(1-\exp{(-t/2)})$$ and$$\frac{dx}{dx_0}=1+2\frac{du_0}{dx_0}(1-\exp{(-t/2)})$$ We want to know the time and place where this first vanishes. This will be where $\frac{du_0}{dx_0}$ takes its most negative value, of $-1$ at $x_0=\pi$, and when $$1-2(1-\exp{(-t/2)})=0$$ which gives you $t_c$.
It might be instructive if you used Mathematica or something to plot the characteristic paths. You would see how they intersect and how they then produce a double covering of the plane.
$$u_t+uu_x=-\frac{1}{2}u $$ Characteristic set of ODEs : $\quad \frac{dt}{1}=\frac{dx}{u}=\frac{du}{-\frac{1}{2}u}$
First characteristic equation, from $\quad \frac{dx}{u}= -2\frac{du}{u} \quad\to\quad u+\frac{1}{2}x=c_1$
Second characteristic equation, from $\quad dt=-2\frac{du}{u}\quad\to\quad ue^{t/2}=c_2$
General solution of the PDE expressed on the form of implicit equation : $$\Phi\left(u+\frac{1}{2}x\:,ue^{t/2}\right)=0$$
where $\Phi$ is any differentiable function of two variables.
Or, equivalently: $u+\frac{1}{2}x=F\left(ue^{t/2}\right)$ $$u=-\frac{1}{2}x+F\left(ue^{t/2}\right)$$
where $F(X)$ is any differentiable function with $X=ue^{t/2}$
CONDITION : $u(x,0)=\sin(x)$
In this condition, $X=ue^{0/2}\quad\to\quad X=u=\sin(x)$.
$x=\sin^{-1}(X)\quad$ Hence $u= -\frac{1}{2}x+F(X)=-\frac{1}{2}\sin^{-1}(X)+F(X) =X$
$$ F(X)=X+\frac{1}{2}\sin^{-1}(X)$$
Now, the function $F$ is determined and can be put into the above general solution, which becomes the particular solution according to the specified condition.
$$u=-\frac{1}{2}x+F\left(ue^{t/2}\right)=-\frac{1}{2}x+\left(X+\frac{1}{2}\sin^{-1}(X)\right)$$ where $X=ue^{t/2}\quad\to\quad u=-\frac{1}{2}x+ue^{t/2}+\frac{1}{2}\sin^{-1}(ue^{t/2})$
$\sin^{-1}(ue^{t/2})=x+2u\left(1-e^{t/2}\right)\quad\to\quad ue^{t/2}=\sin\left(x+2u\left(1-e^{t/2}\right)\right)$ $$u=e^{-t/2}\sin\left(x+2u\left(1-e^{t/2}\right)\right)$$
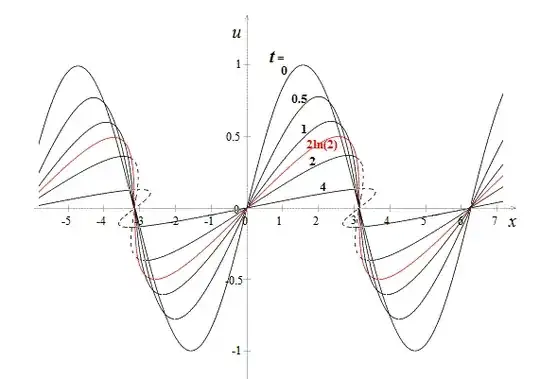
Note that $u(x,t)$ is multivalued for $t>2\ln(2)$ in some range of $x$.
Explanations are provided (for example) in : http://www1.maths.leeds.ac.uk/~kersale/Teach/M3414/Notes/m3414_2.pdf
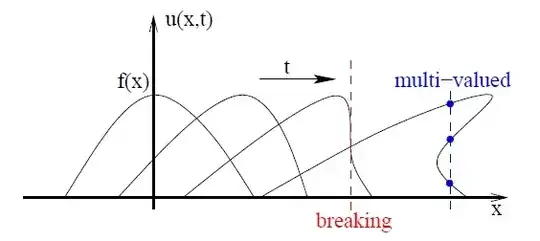
Especially, compare to the next figure taken from this pdf, page 28 :
The shock between states $u_L,u_R$ moves with speed $(u_L+u_R)/2$. This follows from applying conservation to an infinitesimal rectangular control volume that has part of the shock path as a diagonal. The source term has no effect on this. Past the shock formation time, the solution is double-valued, and in this region the shock is governed by the ODE $$\frac{dx_s}{dt}=\frac{1}{2}(u_1+u_2)$$ There will not be an explicit solution to this because $u_{1,2}$ are only given implicitly (but probably that was not what you meant}
