3

I'm trying to find Hessian of $\text{tr}((AB)' (AB))$ where $A,B$ are matrices. There are nice expressions for $H_{AA}$ and $H_{BB}$ using standard approach from Magnus 1 , can anyone suggest how to do same for $H_{AB}$ and $H_{BA}$ ?

More specifically if $A$ is 2x3 and $B$ is 3x4, then we can vectorize A,B and stack them on top of each other so that we have a function from vectors, and Hessian is a block partitioned matrix with blocks 6x6, 6x12, 12x6 and 12x12 corresponding to $H_{AA}$, $H_{AB}$, $H_{BA}$ and $H_{BB}$

Edit (after following techniques in answer, I get following)

$$H_{AA}=2(BB'\otimes I_2)$$ $$H_{BB}=2(I_4 \otimes A'A)$$ $$H_{AB}=2(B\otimes A)+2 (I_3 \otimes AB)K_{3,4}$$ $$H_{BA}=2(B'A'\otimes I_3)K_{2,3}+2(B'\otimes A')$$

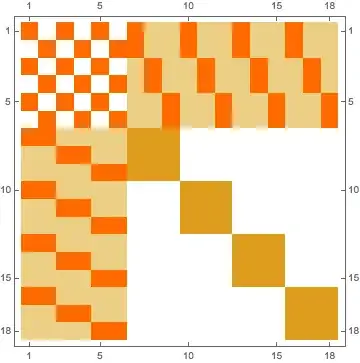
BTW, the Hessian looks as follows when evaluated with all values being 1. Four colors represent values 0,2,4,8 so that $H_{AB}$ consists of just 2's and 8's.

enter image description here

Mathematica code used to generate.

1 (Theorem 1 in 10.6 of Magnus/Nuedecker Matrix Differential Calculus with Applications in Statistics ebook)

Yaroslav Bulatov
  • 5,327

1 Answers1

3

To solve this problem you need the Commutation Matrix that is used to transform Kronecker products. Let's denote it by $K$.

Let $$X=AB$$ and write the function in terms of the inner/Frobenius product (denoted by a colon). Then find the differential and gradient $$\eqalign{ f&= X:X \cr\cr df&= 2X:dX \cr &= 2X:dA\,B + 2X:A\,dB \cr &= 2XB^T:dA + 2A^TX:dB \cr\cr G_A =\frac{\partial f}{\partial A}&= 2XB^T = 2ABB^T \cr G_B =\frac{\partial f}{\partial B}&= 2A^TX = 2A^TAB \cr \cr }$$ Now find the differentials and gradients of these gradients (aka the hessians).

First, the differentials $$\eqalign{ dG_A&= 2(dA\,BB^T+A\,dB\,B^T+AB\,dB^T) \cr dG_B&= 2(dA^T\,AB+A^T\,dA\,B+A^TA\,dB) \cr \cr }$$ Vectorize the differentials $$\eqalign{ dg_A&= 2((BB^T\otimes I)\,da+(B\otimes A)\,db+(I\otimes AB)K\,db) \cr dg_B&= 2((AB\otimes I)^TK\,da+(B\otimes A)^T\,da+(I\otimes A^TA)^T\,db) \cr \cr }$$ By inspection, the hessians are $$\eqalign{ H_{AA}= \frac{\partial g_A}{\partial a}&= 2(BB^T\otimes I) \cr H_{AB}= \frac{\partial g_A}{\partial b}&= 2(B\otimes A)+2(I\otimes AB)K \cr \cr H_{BB}= \frac{\partial g_B}{\partial b}&= 2(I\otimes A^TA) \cr H_{BA}= \frac{\partial g_B}{\partial a}&= 2(B^TA^T\otimes I)K+2(B^T\otimes A^T) \cr \cr }$$

greg
  • 35,825
  • 1
    Also with noting, the commutation matrix is a sparse matrix with a single 1 in each row and zeros elsewhere. It can be constructed by building the matrix that, when vectorised, becomes the vector (1,2,3,4,...). Then transpose that matrix and vectorise it. The i'th entry of the result is the column containing the 1 in the i'th row. See the code at the end of the following post for more details: http://math.stackexchange.com/a/603282/3060 – Nick Alger Mar 28 '17 at 03:15
  • Amazing, thanks! Updated answer with K dimensions and Mathematica code used to verify that this works – Yaroslav Bulatov Mar 28 '17 at 19:00