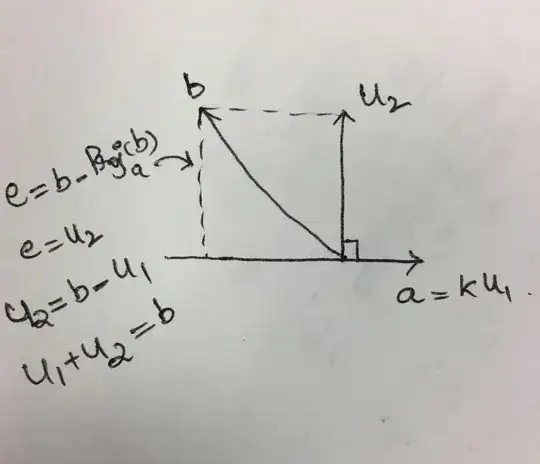
If $a=(12,5)$ and $b=(6,8)$ give two orthogonal vectors $U_1$ and $U_2$ such that $U_1$ lies in $a$ and $U_1+U_2=b$

Question

If $a=(12,5)$ and $b=(6,8)$ give two orthogonal vectors $U_1$ and $U_2$ such that:

$1)$ $U_1$ lies in $a$

$2)$ $U_1+U_2=b$

I am not really sure what the problem is even asking and I would like some assistance in understanding what the problem is asking about.

I have a vague idea on the problem as it is supposed to require some sort of usage of projections but I do not know how projections apply in this problem.

Have you learned about orthogonal projections? – Jean-François Gagnon Mar 24 '17 at 14:22 — Jean-François Gagnon, Mar 24 '17 at 14:22
@Jean-FrançoisGagnon yes – John Rawls Mar 24 '17 at 14:31 — John Rawls, Mar 24 '17 at 14:31

score 1 · Accepted Answer · answered Mar 24 '17 at 15:33

1

Here is my guess:

$U_1$ lies in $a$ would means that $U_1=ka$, $k\in \Bbb R^*$, so $U_2=b-ka$.

Once $U_1$ and $U_2$ are orthogonal then $U_1\cdot U_2=0$ so,

$$U_1\cdot U_2=ka\cdot(b-ka)=ka\cdot b-k^2|a|^2=0\to k=\frac{a\cdot b}{|a|^2}$$

but

$$a\cdot b=(12,5)\cdot (6,8)=72+40=132\\ |a|^2=12^2+5^2=169$$

Now you are able to find $U_1$ and $U_2$.

answered Mar 24 '17 at 15:33

Arnaldo

21,342

could you help me with this question ; http://math.stackexchange.com/questions/2202369/prove-the-given-identity-using-the-shortest-method-possible?noredirect=1#comment4531181_2202369 – Aryabhatta Mar 25 '17 at 12:02

score 1 · Answer 2 · answered Mar 24 '17 at 21:25

1

Just to give you a pictorial view of the problem. ${e}$ is the error.

answered Mar 24 '17 at 21:25

VBJ

141

If $a=(12,5)$ and $b=(6,8)$ give two orthogonal vectors $U_1$ and $U_2$ such that $U_1$ lies in $a$ and $U_1+U_2=b$

2 Answers2