4

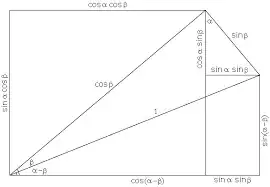
For some reason I'm starting to get nit picky about everything I have learned. In Geometry/ Algebra I learned how to prove the angle sum formulas, which follow from this picture (and a slightly different picture with $a$ and $b$ instead of $\beta$ and $\alpha-\beta$ :

enter image description here

But now that I realize it this argument only works if the angle sum $x$ follows the inequality $0<x<\frac{\pi}{2}$. And every angle is larger than $0$, in radians.

How can we geometrically prove (to a high school student taking algebra/geometry) the trigonometric sum formulas but for all angles?

Definition

Here is what I'll take to be the definition of sine and cosine (if you know of another definition I'd appreciate it if you share):

Let $(x,y)$ be a point in the Cartesian plane, let $\theta$ be the counterclockwise angle in radians from the positive $x$ axis to the segment connecting $(x,y)$ to the origin. Let a clockwise angle of $\theta$ be equivalent to a counterclockwise angle of $-\theta$, and vice versa. Take "sin" and "cos" to be $2\pi$ periodic functions. Let $r$ be the distance from $(x,y)$ to the origin. In other words $r=\sqrt{x^2+y^2}$. Then define:

$$\sin (\theta)=\frac{y}{r}$$

$$\cos (\theta)=\frac{x}{r}$$

Ahmed S. Attaalla
  • 18,518
  • This is very simple to do, if you are willing to accept identities like $sin(90-x)=sin(90+x)$ and such. If you aren't, the proof for this is very straightforward after drawing the unit circle. – Anonymous Pi Mar 21 '17 at 21:58
  • I prefer to start straight from the definitions like sin= opp/hpp or more precisely $\sin (\theta)=\frac{y}{r}$. At least the second is what I think the definition of $\sin (\theta)$ is. @AnonymousPi – Ahmed S. Attaalla Mar 21 '17 at 22:02
  • 1
    You have to go beyond that definition because if you write $\sin \theta=y/r$ you are saying that $\sin \theta >0$ and then you can't prove anything for an angle $\pi <\theta <2\pi$ – Arnaldo Mar 21 '17 at 22:04
  • @AhmedS.Attaalla As Arnaldo says it, you can't prove anything if you restrict yourself to that, because by definition the function for this values will be defined. – Anonymous Pi Mar 21 '17 at 22:13
  • 1
    I have added my definitions please let me know if anything is unnecessary to be defined, and if I need to add anything @AnonymousPi – Ahmed S. Attaalla Mar 21 '17 at 22:40
  • 1
    This answer of mine ---and this one, on which it is based--- may be helpful. – Blue Mar 21 '17 at 22:41
  • 2
    Not to go off on too much of a tangent, but I've seen some authors (Rudin, I believe) define $cos(x)$ and $sin(x)$ functions as the real and complex part, respectively, of $e^{ix}$ (or the series representation of such). I am not aware how much that helps here, but I would be interested to know how many trig identities could be shown by this route. – Thomas Rasberry Mar 21 '17 at 22:51
  • @ThomasRasberry Basically all of them can. Of course, once you prove the geometric connection. – Anonymous Pi Mar 21 '17 at 22:59
  • @AhmedS.Attaalla Using your definitions, it shouldn't be hard to prove the identities relating the sines or cosines of values between 0 and $\frac{\pi}{2}$ to general values. If I'm not wrong, it should be nothing more than triangle congruence. – Anonymous Pi Mar 21 '17 at 23:01

0 Answers0