I describe the problem dimension $2$, but it could be generalized to $n$ dimensions.
So we have $X_{1}, X_{2}, X_{3}$ three $iid$ random variables of continuous law $F(x,y)$ on $\Bbb R^2$. Let's denote by $S[X_{1}, X_{2}, X_{3}]$ the simplex generated by those random variables. Given a point $(x,y)$, is it possible to write $P((x,y)\in S[X_{1}, X_{2}, X_{3}])$ as a function $g$ of $F(x,y)$ ? For example, in dimension $1$, $P(x\in [X_{1}, X_{2}]) = 2F(x)(1-F(x))$.
Thank you
Given any three distinct points $A, B, C$, let
Given any fixed point $P = (x_P,y_P)$ and three random points $X_1, X_2, X_3$ sampled from a continuous distribution. Aside from events of probability zero, the four points $P, X_1, X_2, X_3$ will be in general position. i.e. no three of them will be colinear. Let $Y_1, Y_2, Y_3$ be a reordering of the $X_1, X_2, X_3$ so that $Y_1, Y_2, Y_3$ surrounds the triangle $\triangle_{X_1X_2X_3}$ in counterclockwise manner.
There are four mutually exclusive possibilities for the position of $P$ relative to $Y_1, Y_2, Y_3$. $P$ can lie in the interior of triangle $\triangle_{Y_1Y_2Y_3}$ or interior of one the cones $\color{red}{\mathcal{C}(Y_1,Y_3,Y_2)}, \color{green}{\mathcal{C}(Y_2,Y_1,Y_3)}$ and $\color{blue}{\mathcal{C}(Y_3,Y_2,Y_1)}$.
$\hspace{1in}$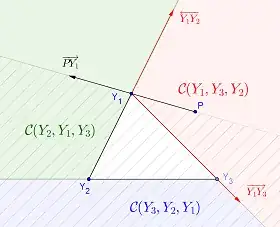 
There is a simple criterion to test whether $P$ belongs to one of the cones.
As one can see from above diagram, $P \in \mathcal{C}(Y_1,Y_3,Y_2)$ is more or less equivalent to both $Y_2,Y_3$ lie at "left hand" side of ray $\overrightarrow{PY_1}$ (the hatched area in above diagram ). This happens to the other two cones. Aside from events of probability zero, we have $$ \begin{align} P \in \mathcal{C}(Y_1,Y_3,Y_2)\quad\iff\quad Y_2,Y_3 \in \mathcal{H}(P,Y_1)\\ P \in \mathcal{C}(Y_2,Y_1,Y_3)\quad\iff\quad Y_3,Y_1 \in \mathcal{H}(P,Y_2)\\ P \in \mathcal{C}(Y_3,Y_2,Y_1)\quad\iff\quad Y_1,Y_2 \in \mathcal{H}(P,Y_3) \end{align} $$
Using symmetry and the fact $X_1, X_2, X_3$ are $iid$ from same continuous distribution, we have
$$ \mathbb{P}\left[P \in \triangle_{X_1X_2X_3}\right] = 1 - 3\mathbb{P}\left[ Y_2,Y_3 \in \mathcal{H}(P,Y_1) \right] = 1 - 3\mathbb{E}\left[ \mathbb{P}\left[ X_2 \in \mathcal{H}(P,X_1) | X_1 \right]^2 \right]$$
This leads to following integral representation of the desired probability $$\mathbb{P}\left[P \in \triangle_{X_1X_2X_3}\right] = 1 - 3\int_{0}^{2\pi} \rho(P,\theta) \left[ \int_{\theta}^{\theta+\pi}\rho(P,\phi)d\phi \right]^2 d\theta $$ where $$\rho(P,\theta)\stackrel{def}{=} \int_{0}^{\infty}F(x_P+r\cos\theta,y_P+r\sin\theta) rdr$$ is the probability density function for ray $\overrightarrow{PX_1}$ making an angle $\theta$ with respect to the $x$-axis.
There is an interesting special case. When $F(x,y)$ is centrally symmetric with respect to $P$, $$\mathbb{E}\left[X_2 \in \mathcal{H}(P,X_1) | X_1\right] = \int_{\theta}^{\theta+\pi} \rho(P,\phi)d\phi = \frac12$$ independent of $\theta$. In that case, we have $$\mathbb{P}\left[P \in \triangle_{X_1X_2X_3}\right] = 1 - 3\left(\frac12\right)^2 = \frac14 $$
This is based on the barycentric coordinates. Applying Cramer's rule or using suitable software, one obtains \begin{aligned} a_1 &= \frac{x_2 y_3 - y_2 x_3 + x_3 y - x y_3 - x_2 y + y_2 x}{-x_2 y_1 + x_2 y_3 - x_1 y_3 + y_1 x_3 + y_2 x_1 - y_2 x_3} \, , \\ \\ a_2 &= \frac{x_1 y - x_1 y_3 - x_3 y + y_1 x_3 + x y_3 - y_1 x}{-x_2 y_1 + x_2 y_3 - x_1 y_3 + y_1 x_3 + y_2 x_1 - y_2 x_3} \, , \\ \\ a_3 &= \frac{-x_2 y_1 - x_1 y + y_1 x + x_2 y + y_2 x_1 - y_2 x}{-x_2 y_1 + x_2 y_3 -x_1 y_3 + y_1 x_3 + y_2 x_1 - y_2 x_3} \, , \end{aligned} where $X_i=(x_i,y_i)$ and $X=(x,y)$. It does not look like there is a simple rule to find the law of $a_i$, but the denominators in $\lbrace a_1, a_2, a_3\rbrace$ are all the same, and the numerators are very similar. One may view the problem with a different point of view. Indeed, one can compute the edge lines of the triangle: \begin{aligned} E_{12}: & \;\left(y - y_1\right) \left(x_2 - x_1\right) = \left(y_2 - y_1\right) \left(x - x_1\right) \, , \\ E_{13}: & \;\left(y - y_1\right) \left(x_3 - x_1\right) = \left(y_3 - y_1\right) \left(x - x_1\right) \, , \\ E_{23}: & \;\left(y- y_2\right) \left(x_3 - x_2\right) = \left(y_3 - y_2\right) \left(x - x_2\right) \, . \\ \end{aligned} The point $X=(x,y)$ belongs to the triangle if $X$ belongs to the same half-plane as $X_3$ with respect to $E_{12}$: \begin{aligned} \text{sign}\left(\left(y - y_1\right) \left(x_2 - x_1\right) - \left(y_2 - y_1\right) \left(x - x_1\right)\right) = \text{sign}\left(\left(y_3 - y_1\right) \left(x_2 - x_1\right) - \left(y_2 - y_1\right) \left(x_3 - x_1\right)\right) , \end{aligned} etc. The latter equation is not very different from $a_3\geq 0$.
