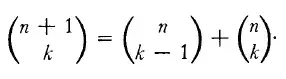Question: Prove the Binomial theorem: if $a$ and $b$ are any numbers and $n$ is a natural number, then:
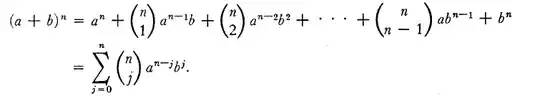
The Proof:
I was able to derive up to the last line of the proof, but am confused about the final line where after factoring the summation using the expression:
I do not understand why exactly they set the upper limit of the summation in the final line to $j= n +1 $ . The second to last line also has the upper limit of $j = n$ in the first part of the summation. Does it not matter? Or is it because, I am allowed to set the limit in such a way so that the last line's equation holds, in which case the limit makes sense. Am I missing something?