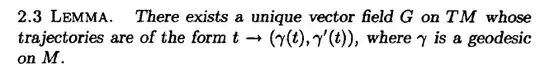6

I understand what a geodesic is, but I'm struggling to understand the meaning of the geodesic flow (as defined e.g. by Do Carmo, Riemannian Geometry, page 63).

I can state my confusion in two different ways:

1)

Do Carmo writes:

enter image description here

Why does a geodesic $\gamma$ uniquely define a vector field on an open subset? In other words, why are the values of the vector fields uniquely defined on those points that are not on the geodesic $\gamma$?

2)

In local coordinates, the geodesic flow is defined as the solution to the ordinary differential equation

$$ \tag{1}\frac{d^2 x_k}{dt^2}+\sum_{i,j}\Gamma^k_{ij}\frac{dx_i}{dt}\frac{dx_j}{dt}=0 $$

For the solution to be unique on $TM$ (or on an open subset), we need some boundary condition. The only boundary condition I can see is a given geodesic $\gamma(t)$.

What are the boundary conditions for this ODE?

Andy Miles
  • 911

1 Answers1

3

The basic idea behind the approach Do Carmo takes is to interpret a curve $(\gamma(t), \gamma'(t))$ where $\gamma \colon [a,b] \rightarrow M$ is a geodesic in $M$ as an integral curve of a globally defined vector field $G$ on $TM$. Once you do that, in order to show the existence of a geodesic $\gamma$ with $\gamma(0) = p$ and $\gamma'(0) = v$ (with $v \in T_pM$) you can take an integral curve $\beta \colon (a,b) \rightarrow TM$ of $G$ with $\beta(0) = (p,v)$ and then the projection $\gamma := \pi \circ \beta$ of $\beta$ to $M$ will be a geodesic which satisfies the initial conditions $\gamma(0) = p$ and $\gamma'(0) = v$.

The uniqueness of geodesics will follow from the uniqueness of integral curves of the vector field $G$, once a starting point $(p,v) \in TM$ is specified. There is no need to impose boundary conditions (and in general, an ODE with boundary conditions might have no solutions satisfying arbitrary boundary conditions), only initial conditions.

levap
  • 65,634
  • 5
  • 79
  • 122
  • 1
    Thank you, but I'm still at the same problem. Yes, the geodesic defines the vector field on the image of the geodesic, i.e. on the points $p$ that are on the geodesic. But take a point $\bar p$ which is not on the geodesic. How is the vector field at $\bar p$ defined? – Andy Miles Mar 20 '17 at 21:22
  • @AndyMiles: It's not that a specific geodesic defines the vector field on the image of the geodesic, it's the geodesic equation which defines a vector field on $TM$ according to the formula given in Do Carmo. – levap Mar 20 '17 at 21:28
  • 1
    Getting more confused. Are we talking about one vector field for all geodesics, or one vector field for each geodesic? In other words, does Do Carmo's lemma say "for each given geodesic $\gamma$, there is a unique vector field such that...", or does it say "there is one unique vector field such that for each geodesic $\gamma$ ..."? Is it $\forall\gamma\exists G$ or $\exists G\forall\gamma$? – Andy Miles Mar 20 '17 at 21:31
  • @AndyMiles: The point is that there is one vector field whose integrals curves gives you all the geodesics. If you prefer to think about it in another way, assume first that all geodesics exist for a short time. For each $(p,v) \in TM$, consider a geodesic $\gamma(t)$ with $\gamma(0) = p$ and $\gamma'(0) = v$. Then $\beta(t) = (\gamma(t), \gamma'(t))$ is a curve in $TM$ and you want to find a vector field $G$ which is globally defined on $TM$ such that $\beta$ is an integral curve of $G$. – levap Mar 20 '17 at 21:36
  • That is, $\beta'(t) = G(\beta(t))$ so $G$ is determined on the image of $\beta$. Since we assumed that all geodesics exist, we know the value of $G$ at all the points of $TM$ and it is well-defined because a geodesic, being a solution of a second order ODE, should be determined uniquely by the initial values. Now, in order to prove existence and uniqueness of geodesics, the logic is reversed. We construct $G$ explicitly and then the projection of the integral curves of $G$ will be geodesics. – levap Mar 20 '17 at 21:36
  • Uh, when you're saying "vector field defined on TM", do you mean a vector field on the bundle of vector fields? So for each pair $(p,v)$ it assigns a "vector-vector" $(\dot p,\dot v)$, right? I think my problem is that I thought of it as just a vector field on $M$, instead of one on $TM$. – Andy Miles Mar 20 '17 at 21:39
  • @AndyMiles: Yeah, more precisely, a vector field on the bundle of tangent vectors, not vector fields. So yes, for each pair $(p,v) \in TM$ it assigns a tangent vector in $T_{(p,v)}(TM)$. There's no chance to get a vector field on $M$ because a geodesic is not determined uniquely but the initial position, only by the initial position and velocity. That's why we need to lift everything to $TM$. This is very similar to the trick of reducing a second order equation to a pair of first order equations by introducing a formal variable and another equation. – levap Mar 20 '17 at 21:42
  • 1
    Thank you! Such a vector field seems better suited to accommodate for all geodesics than just a vector field on $M$ :-) – Andy Miles Mar 20 '17 at 21:44