3

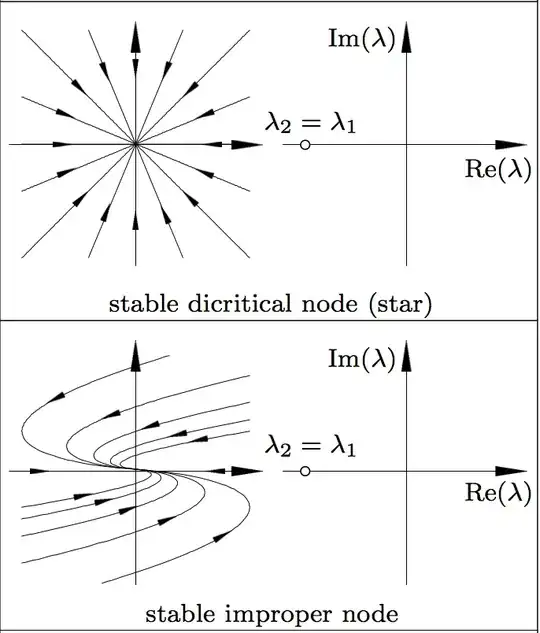
I am analyzing the stability of 2-dimensional flows. If my two eigenvalues are the same, I either have a degenerate node, if I have only one eigenvector or, if I have two distinct eigenvectors, I have a dicritical node.

enter image description here

However, when searching for 2x2 matrices with algebraic multiplicity 2 and two distinct eigenvectors I could only find the identity matrix and multiples.

Are there other matrices with these characteristics in the 2d case?

McLawrence
  • 204
  • 4
    If you have two linearly independent eigenvectors, then every (non-null) vector is an eigenvector (since we are in 2D). This implies that the transformation is a scalar multiple of the identity, for a proof of this, see (https://math.stackexchange.com/questions/1090362/if-every-vector-is-an-eigenvector-the-operator-must-be-a-scalar-multiple-of-the). – Eman Yalpsid Mar 20 '17 at 17:33

0 Answers0