6

I have studied EigenValues and EigenVectors but still what I can't see is that how EigenVectors become transformed or rotated vectors.

user122358
  • 2,712

2 Answers2

11

Matrix as a map

How does a matrix transform the locus of unit vectors?

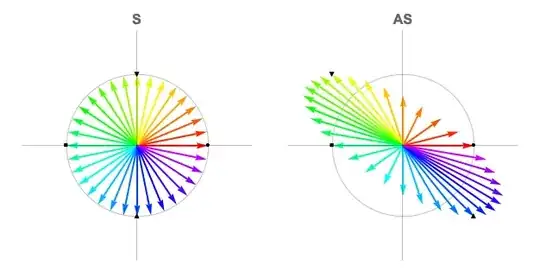
Pick an example matrix such as $$ \mathbf{A} = \left[ \begin{array}{rr} 1 & -1 \\ 0 & 1 \\ \end{array} \right]. $$ As noted by @Widawensen, a convenient representation of unit circle is the locus of vectors $\mathbf{S}$: $$ \mathbf{S} = \left[ \begin{array}{l} \cos \theta \\ \sin \theta \end{array} \right], \quad 0 \le \theta \lt 2\pi $$ The matrix product shows the mapping action of the matrix $\mathbf{A}$: $$ \mathbf{A} \mathbf{S} = \left[ \begin{array}{cc} \cos (\theta )-\sin (\theta ) \\ \sin (\theta ) \end{array} \right] $$

The plots below show the colored vectors from the unit circle on the left. On the right we see how the matrix $\mathbf{A}$ changes the unit vectors.

Matrix as map

Singular value decomposition

To understand the map, we start with the singular value decomposition: $$ \mathbf{A} = \mathbf{U} \, \Sigma \, \mathbf{V}^{*} $$ The beauty of the SVD is that every matrix has a singular value decomposition (existence); the power of the SVD is that it resolves the four fundamental subspaces.

The singular value decomposition is an eigendecomposition of the matrix product $\mathbf{A}^{*} \mathbf{A}$. The singular values are the square root of the nonzero eigenvalues $$ \sigma \left( \mathbf{A} \right) = \sqrt{ \lambda \left( \mathbf{A}^{*} \mathbf{A} \right) } $$ The singular values are, by construction, positive and are customarily ordered. For a matrix of rank $\rho$, the expression is $$ \sigma_{1} \ge \sigma_{2} \ge \dots \ge \sigma_{\rho} > 0 $$ The normalized eigenvectors are the column vectors of the domain matrix $\mathbf{V}$. The column vectors for the codomain matrix $\mathbf{U}$ are constructed via $$ \mathbf{U}_{k} = \sigma_{k}^{-1} \left[ \mathbf{A} \mathbf{V} \right]_{k}, \quad k=1,\rho. $$

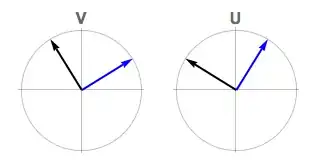
Graphically, the SVD looks like this:

Domain matrices from SVD

The first column vector is plotted in black, the second in blue. Both coordinate systems are left-handed (determinant = -1). The SVD orients these vectors to align the domain and the codomain.

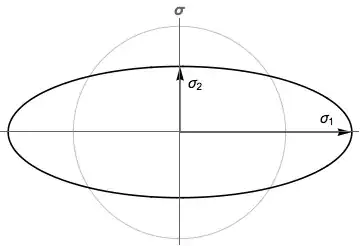
Notice in the mapping action that some vectors shrink, others grow. The domain and codomain have different length scales, and this is captured in the singular values. Below, the singular values are represented as an ellipse with equation $$ \left( \frac{x}{\sigma_{1}} \right)^{2} + \left( \frac{y}{\sigma_{2}} \right)^{2} = 1. $$

Ellipse of singular values

SVD and the map

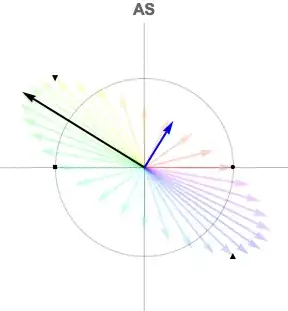
Finally, we bring the pieces together by taking the map image $\mathbf{A}\mathbf{S}$ and overlaying the basis vectors from the codomain $\mathbf{U}$, scaled by the singular values.

Map with U vectors

The black vector is $\sigma_{1} \mathbf{U}_{1}$, blue is $\sigma_{2} \mathbf{U}_{2}$.

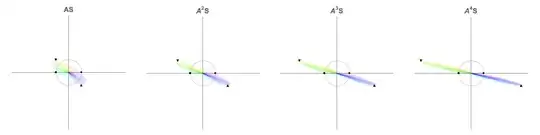
Powers

Repeated applications of the map accentuate the effects of the map. For this example $$ \mathbf{A}^{k} = \left[ \begin{array}{cr} 1 & -k \\ 0 & 1 \\ \end{array} \right], \quad k = 1, 2, 3, \dots $$ The first maps in the sequence are shown below on a common scale:

enter image description here

dantopa
  • 10,342
  • Which one is the eigenvector? – user122358 Mar 17 '17 at 17:02
  • @user122358 Great idea. Modifying drawings to show that. – dantopa Mar 17 '17 at 18:56
  • @user122358 Unfortunately, the given matrix has no real eigenvectors. – amd Mar 17 '17 at 21:49
  • @amd What about $ (1,0)^T vector$ ? – Widawensen Mar 18 '17 at 04:51
  • 1
    @dantopa Very interesting idea - to use different values of hue to represent directions of vectors, maybe saturation or intensity from HSi model of color could be used to show eigenvectors - $( 1,0)^T$ in this case. – Widawensen Mar 18 '17 at 04:58
  • @Widawensen That’s an eigenvector only for a few select values of $\theta$. The pictured mapping is just the effect of $\mathbf A$ or, if you prefer, $\mathbf A\mathbf S_2$ with $\theta=0$. This isn’t terribly surprising since the rotation only has real eigenvectors for a only a few values of the angle, too. – amd Mar 18 '17 at 05:13
  • @user122358 Imagine that the matrix is some kind of amplifier which amplifies vectors - Dantopa's ilustration is very instructive - and some vectors are amplified without change of directions - these are real eigenvectors. – Widawensen Mar 18 '17 at 05:16
  • @amd Eigenvector here is for $A$ transformation - $S_2$ shows only a bunch of vectors to be transformed - the picture - as I understand it - seems to represent vectors for all values of $\theta$ from $0$ to $2\pi$. – Widawensen Mar 18 '17 at 05:21
  • @dantopa However I don't know why you choose a whoole matrix $S_2$ ( two orthogonal to each other column vectors) for representing a unit circle - a single vector $[\cos(\theta), \sin(\theta)]^T$ would be enough.. – Widawensen Mar 18 '17 at 05:34
  • 3
    +1 and I wish I could give more for the beautiful visuals and favorited the question so I can come back to look at the graphs if I need! –  Mar 18 '17 at 20:50
  • @Widawensen: Vector instead of matrix is a better idea. Thanks. – dantopa Mar 18 '17 at 21:26
  • 3
    @dantopa You have fantastically developed your answer. I think such ingenuity deserves more than +50. Unit circle seems to be very good as illustrative example.. – Widawensen Mar 20 '17 at 16:55
2

Linear maps $T:\>V\to W$ make sense between any two vector spaces $V$, $W$ over the same ground field $F$.

The notions of eigenvalues and eigenvectors only make sense for linear maps $T:\>V\to V$ mapping some vector space $V$ into itself. A vector $v\ne0$ that is "by coincidence" mapped onto a scalar multiple $\lambda v$ of itself is called an eigenvector of $T$. Such a vector is maybe shrinked or stretched by $T$, but it is not "rotated" or "sheared" in any way. The numbers $\lambda$ occurring in such circumstances are called eigenvalues of $T$. It is a miracle that (in the finite dimensional case) a given $T$ may only have a finite number of eigenvalues.

Christian Blatter
  • 226,825