-1

I've seen the proof of $\lim_{x\rightarrow0} \frac{\sin(x)}{x}=1$ but it uses the fact that $\tan(x)>x$ which in all places says it is obvious but this is maths and a I'd like to see a purely rigorous proof. If anyone knows about please comment and thanks in advance.

miracle173
  • 11,049
J. P. C.
  • 155

2 Answers2

4

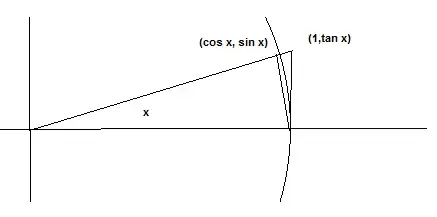
enter image description here

We have three regions.... The triangle with vertexes $(0,0), (1,0), (\cos x, \sin x)$

Area $=\frac 12 |\sin x|$

The section of the circle with angle $x$

Area $=\frac 12 |x|$

The triangle with vertexes $(0,0), (1,0), (1, \tan x)$

Area $=\frac 12 |\tan x|$

Each is entirely inside the next region.

$\frac 12|\sin x|\le\frac 12|x|\le\frac 12|\tan x|$

Doug M
  • 57,877
1

Pictorially: enter image description here To see why the inequality holds, consider the areas of triangles and the arc.

After one has built sufficient calculus, we can give the following proof: write the Mean Value Theorem for the function $f(t)=\tan t,$ over the interval $[0,x]$, where $0<x<\pi/2$: $$\frac{\tan x -\tan 0}{x-0}=1 + \tan ^2 c \geq 1.$$ There you are!

Behnam Esmayli
  • 5,024
  • 1
    Your second proof does not work, because you need $\lim \frac {\sin x}x = 1$ to find the derivative of $\sin, \cos$, and therefore $\tan$. Which makes that proof circular. – Paul Sinclair Mar 14 '17 at 23:50
  • @PaulSinclair Actually it depends on your definition of the trigonometric functions. If you define them by means of the exponential function on the complex plane then you can compute the derivatives from the definition. If, instead, you define them geometrically, then I think that you are forced to show that $\tan x > x$ using geometric arguments. – Matteo Menghini Sep 08 '22 at 09:10
  • 1
    @MatteoMenghini - yes there are many ways one could define the trig functions which would bring with it an automatic existence of derivatives, and likely an a easy proof that $\lim_{x\to 0} \frac{\sin x}x = 1$. However, there are only two ways that trig functions are first defined for practically everyone: by triangle for angles between $0$ and $\frac \pi 2$ and then by unit circle to extend them to other angles. And this is very clearly the definitiion in use by the OP and by this poster. Esoteric alternate definitions are not what the OP was after. – Paul Sinclair Sep 08 '22 at 17:13