3

Given the matrix:

$$ A=\begin{pmatrix} 3 & 1 \\ -1 & 2 \\ \end{pmatrix}. $$

Let $V =\mathbb Z^2$ and $L = AV$. We want to find basis for $V$ and $L$ and draw the sublattice that exhibit the diagonalization.

I found the diagonal form of the matrix to be:

$$\begin{pmatrix} 1 & 0 \\ 0 & -7 \\ \end{pmatrix}$$

I think we need that because the solution says the basis for $V$ is $\{(1,2) , (0,1)\}$ while the basis for $L$ is $\{(1,2),(0,7)\} $.

But it says we can conclude that from the sublattice. So, can someone briefly point out how I can sketch the sublattice?

EDIT:

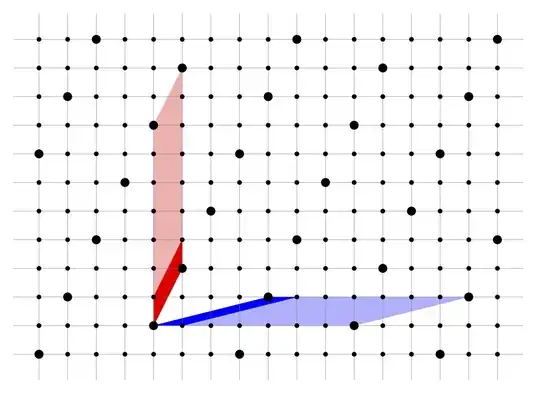
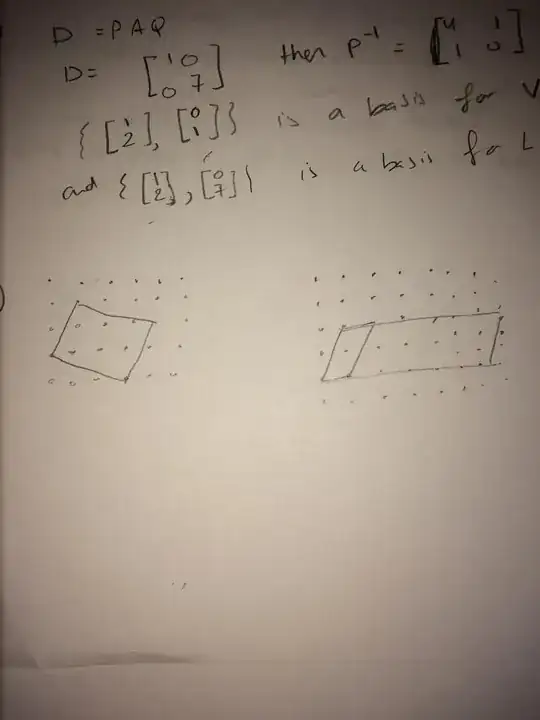
enter image description here

Also my attempt at drawing it: enter image description here

user26857
  • 52,094
Lana
  • 824
  • 1
    Do you mean that $A$ is your name for the first matrix you display and $V$ is the module $\mathbb Z^2$? And how did you find that purported diagonalized matrix? It doesn't have the same determinant as the original one ($-7$ versus $7$), doesn't have the same trace ($-6$ versus $5$), and neither $1$ nor $-7$ are eigenvalues as far as I can see. – hmakholm left over Monica Mar 14 '17 at 18:29
  • @HenningMakholm I think the OP has correctly calculated the Smith normal form of the given matrix. Why should quantities such as the determinant, trace, or eigenvalues be preserved under this transformation? – Viktor Vaughn Mar 14 '17 at 20:19
  • @Quasicoherent: Hmm, possibly. I was thrown off by the matrix being described as the "diagonalization" of the matrix. – hmakholm left over Monica Mar 14 '17 at 20:22
  • In my textbook they call it the "diagonal form" sorry about that! – Lana Mar 14 '17 at 20:23
  • @HenningMakholm Ah okay, I see why that is confusing. Computing the Smith normal form corresponds to changing bases in both the domain and codomain of the linear map, so it's not like usual diagonalization where we choose the same basis in both the domain and codomain. – Viktor Vaughn Mar 14 '17 at 20:25

1 Answers1

1

The row and column operations you use in computing the Smith normal correspond to invertible matrices $P,Q \in \operatorname{GL}_2(\mathbb{Z})$ such that $$ D = PAQ $$ where $D$ is the diagonal matrix you found. (Since $-1$ is invertible in $\mathbb{Z}$, we can actually take $D$ to be $$ D = \begin{pmatrix} 1 & 0\\ 0 & 7\end{pmatrix} $$ which is what I will use for the rest of the answer.) In this case, I get $$ D = \left(\begin{array}{rr} 1 & 0 \\ 0 & 7 \end{array}\right) \qquad P = \left(\begin{array}{rr} 0 & 1 \\ 1 & -4 \end{array}\right) \qquad Q =\left(\begin{array}{rr} 1 & 2 \\ 1 & 1 \end{array}\right) \, . $$

We can interpret these as change of basis matrices for $V$. (For more on this, see this post or this post.) The change of basis matrix $P$ contains the information we seek: since $P^{-1} = \begin{pmatrix} 4 & 1\\ 1 & 0\end{pmatrix}$, then the set $$ \{v_1, v_2\} = \left\{\begin{pmatrix} 4\\ 1\end{pmatrix}, \begin{pmatrix} 1\\ 0\end{pmatrix}\right\} $$ is a basis for $V$ such that $L = v_1 \mathbb{Z} \oplus 7v_2 \mathbb{Z}$.

As for drawing the sublattice, take a look at pp. 4-5 of this set of notes by Keith Conrad. He draws a lattice and sublattice with respect to so-called unaligned and aligned bases, which I've copied below.

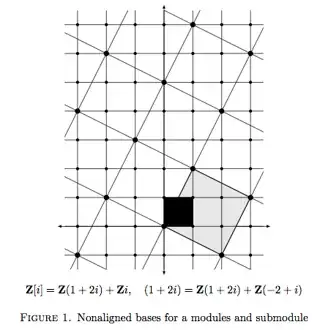
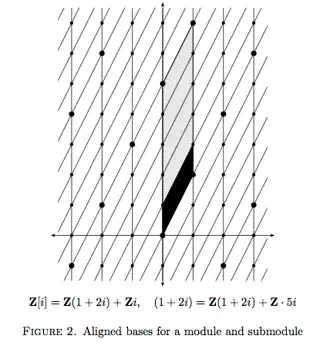
enter image description here enter image description here

I think this is the sort of picture you have in mind. All right, below is my attempt at drawing the lattice $V$ and its sublattice $L$. The blue parallelograms are the fundamental parallelograms of $V$ and $L$ using my basis, and the red is the same for the book's. This shows quite clearly that both answers are correct.

enter image description here

Community
  • 1
Viktor Vaughn
  • 19,278
  • It's {(1,2),(0,1)} that's a basis for v, no? – Lana Mar 14 '17 at 23:03
  • That's not what I got. I'll edit to add a few more details. Could this be a result of you choosing $-7$ rather than $+7$ as the bottom-right entry of $D$? – Viktor Vaughn Mar 14 '17 at 23:08
  • I just added the sample answer – Lana Mar 14 '17 at 23:10
  • ok I tried to draw according to your reference lol.. not the prettiest drawing – Lana Mar 14 '17 at 23:17
  • I have a feeling that both my answer and the book's are correct, meaning that the answer is not unique. You can see that $(4,1)^T$ and $(7,0)^T$ definitely generate $L$ since $(3,-1)^T = (7,0)^T - (4,1)^T$ and $(1,2)^T = 2 \cdot (4,1)^T - (7,0)^T$, so my answer works. – Viktor Vaughn Mar 14 '17 at 23:26
  • Oh ok that's fine. Do you think that's how we draw a sublattice? (not sure if i completely failed at this) – Lana Mar 14 '17 at 23:33
  • I think you drew $(1,0)$ instead of $(0,1)$ in your picture... – Viktor Vaughn Mar 14 '17 at 23:35
  • To draw the lattice, draw the parallelogram with vertices $0,v_1,v_2$, and $v_1+v_2$. For the sublattice, the vertices are instead $0, v_1, 7v_2$, and $v_1+7v_2$. – Viktor Vaughn Mar 14 '17 at 23:41
  • oh ok, should the lattice and sublattice be separate? or the same diagram? – Lana Mar 14 '17 at 23:47