1

Given the a data set with 4 equations with x1, x2 as main drivers.

A) Can there be a unique multilinear model s(x1,x2) = B0+ B1x1+ B2x2 that perfectly fits the data.

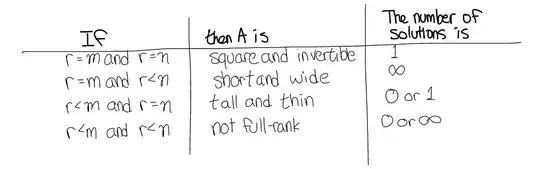
Even before putting the equations into MAtLab, I assumed there could NOT be a unique solution because there are more equations than variables.

B) I followed the same logic when asked to fit the data to the equation: B0 + B1x1 + B2x2 + B3x1x2

Since there are three variables and still 4 equations, there could not be a unique solution...Is this logic correct?

and when asked for to fit the data to the model: B0 + B1x1 + B2x2 + B3x1x2 + B4(x1^2) + B4 (x2^2)..I was not sure because now there are more variables than equations. There could be a unique solution I believe.

x1= avg. temp x2=median income Additional info: the data set Year, Avg. Temp, Median Income, and Total Sales

2009 86.92 30.11 27.93

2010 88.51 31.48 28.29

2011 88.01 32.03 29.70

2012 87.05 33.34 31.09

M. Steven
  • 25
  • Sure there can be a model that perfectly fits your data - this depends on the underlying structure of your data (if there is some simple correlation, a simple model would do). Or am I misunderstanding your question? – Bobson Dugnutt Mar 14 '17 at 17:50
  • http://math.stackexchange.com/questions/1388766/least-squares-fit-for-an-underdetermined-linear-system/2170998#2170998 – dantopa Mar 14 '17 at 22:35

2 Answers2

1

A

Problem specification: Start with a sequence of $m=4$ measurements $\left\{ x_{k}, y_{k}, z_{k} \right\}_{k=1}^{m}$. Use the method of least squares to find the best trial function $$ z(x,y) = b_{0} + b_{1}x + b_{2}y. $$ That is, find the solution vector $b$ defined as $$ b_{LS} = \left\{ b \in \mathbb{C}^{m} \colon \lVert \mathbf{A}b - z \rVert_{2}^{2} \text{ is minimized} \right\}. $$

Your problem has full column rank, so the least squares solution will be unique (the null space $\mathcal{N}\left( \mathbf{A} \right)$ is trivial. $$ \begin{align} \mathbf{A} b & = z \\ \left[ \begin{array}{ccc} 1 & x_{1} & y_{1} \\ 1 & x_{2} & y_{2} \\ 1 & x_{3} & y_{3} \\ 1 & x_{4} & y_{4} \end{array} \right] % \left[ \begin{array}{c} b_{0} \\ b_{1} \\ b_{2} \end{array} \right] % &= % \left[ \begin{array}{c} z_{1} \\ z_{2} \\ z_{3} \\z_{4} \end{array} \right] % \end{align} $$

Because the matrix has full column rank, we may solve directly with the normal equations: $$ b_{LS} = \left( \mathbf{A}^{*} \mathbf{A} \right)^{-1} \mathbf{A}^{*} z. $$

B

The new trial function $$ z(x,y) = a_{00} + a_{10}x + a_{01}y + a_{20} x^{2} + a_{20} x y + a_{20} y^{2} $$ is complete through second order and involves finding $n=6$ coefficients. We no longer have full column rank and the solution is not unique. $$ \begin{align} \mathbf{A} a & = z \\ \left[ \begin{array}{ccc} 1 & x_{1} & y_{1} & x_{1}^{2} & x_{1}y_{1} & y_{1}^{2} \\ 1 & x_{2} & y_{2} & x_{2}^{2} & x_{2}y_{2} & y_{2}^{2} \\ 1 & x_{3} & y_{3} & x_{3}^{2} & x_{3}y_{3} & y_{3}^{2} \\ 1 & x_{4} & y_{4} & x_{4}^{2} & x_{4}y_{4} & y_{4}^{2} \\ \end{array} \right] % \left[ \begin{array}{c} a_{00} \\ a_{10} \\ a_{01} \\ a_{20} \\ a_{20} \\ a_{20} \end{array} \right] % &= % \left[ \begin{array}{c} z_{1} \\ z_{2} \\ z_{3} \\z_{4} \end{array} \right] % \end{align} $$ The general least squares solution for this problem is $$ a_{LS} = \color{blue}{\mathbf{A}^{\dagger}z} + \color{red}{\left( \mathbf{I}_{6} - \mathbf{A}^{\dagger} \mathbf{A} \right) \zeta} , \qquad \zeta \in\mathbb{C}^{6}. $$ where blue vectors are in a $\color{blue}{range}$ space, and red vectors are in a $\color{red}{null}$ space.

dantopa
  • 10,342
  • I'm sorry...However insightful and perhaps brilliant that answer is, I was hoping for perhaps a novice explanation. I was thinking something along the lines of using an augmented matrix with the b vector as the sales and determine if the model could be fit to that particular b vector. – M. Steven Mar 14 '17 at 18:32
  • Look at the column rank to establish uniqueness. If the number of linearly independent columns $\ge$ number of fit parameters, the solution is unique. A) Can there be a unique .. model s? Yes Can there be a unique .. model .that perfectly fits the data? Yes – dantopa Mar 14 '17 at 18:35
1

If you have more equations than variables, then there is a possibility that there won't be any solutions (though, as the other answer indicates, we can find a best fit). We could also have exactly one solution, or infinitely many.

If there are more variables than equations, then again: it is possible that there is no solution. However, there are necessarily infinitely many solutions.

I found a table in my notes that you might find useful. In the below, the matrix is $m \times n$ ($m$ equations and $n$ variables), and $r$ denotes the rank of the associated matrix.

enter image description here

Ben Grossmann
  • 225,327