Get a good approximation of $\int_0^1 \left(H_x\right)^2 dx$, where $H_x$ is the generalized harmonic number

Question

The code

integrate (H_x)^2 dx, from x=0 to x=1

in Wolfram alpha online calculator, where as you see $H_x$ is a generalized harmonic number, tell us that holds $$\int_0^1 \left(H_x\right)^2 dx\approx 0.413172.$$

I've curiosity about

Question. How one can calculate with analysis or numerical analysis an approximation of $$\int_0^1 \left(H_x\right)^2 dx?$$ Thus you are able to use your knowledges about the harmonic numbers, or well if your approach is using numerical analysis tell us what's your numerical method and how works it. Many thanks.

Answer 1

^{This is an interesting question that can be tackled in many ways, there are many chances a good piece of math will come out of it. For now, I will just keep collecting and rearranging observations, till reaching a complete answer.}

We have $H_x=\gamma+\psi(x+1)$ and $\int_{0}^{1}\psi(x+1)\,dx = \log\frac{\Gamma(2)}{\Gamma(1)}=0$, hence our integral equals $\gamma^2+\int_{0}^{1}\psi(x+1)^2\,dx$. The function $\psi(x+1)^2$ is positive and convex on $(0,1)$ and values of the $\psi$ function at rational points in $(0,1)$ can be computed in a explicit way through Gauss' Digamma Theorem, hence the numerical evaluation of the given integral is pretty simple through Simpson's rule or similar approaches.

In a right neighbourhood of the origin we have $$ H_x = \zeta(2)x-\zeta(3)x^2+\zeta(4)x^3-\zeta(5)x^4+\ldots\tag{1} $$ hence $$ \int_{0}^{1}H_x^2\,dx = \sum_{m,n\geq 2}\frac{(-1)^{m+n}}{m+n-1}\zeta(m)\zeta(n) = \sum_{j\geq 3}\frac{(-1)^{j+1}}{j}\sum_{k=2}^{j-1}\zeta(k)\,\zeta(j+1-k) \tag{2}$$ where we may recall Euler's theorem about $\sum_{n\geq 1}\frac{H_n}{n^q}$: $$ \sum_{k=2}^{j-1}\zeta(k)\,\zeta(j+1-k) = (2+j)\,\zeta(j+1)-2\sum_{n\geq 1}\frac{H_n}{n^j}=j\,\zeta(j+1)-2\sum_{n\geq 1}\frac{H_{n-1}}{n^j}. \tag{3}$$ This approach should allow us to convert the original integral into a simple series, since $$ \sum_{j\geq 3}(-1)^{j+1}\zeta(j+1) \stackrel{\text{Abel reg.}}{=} 1-\zeta(2)+\zeta(3).$$ In particular, the problem boils down to the approximation/evaluation of the following series: $$ \sum_{n\geq 1}\left[\frac{1-2n}{2n^2}+\log\left(1+\frac{1}{n}\right)\right]H_{n-1} \tag{4}$$ whose general term yet behaves like $\frac{\log n}{n^3}$, leading to pretty fast convergence.
If we apply summation by parts, we get a general term that is simpler but with a slower decay towards zero: $$ \begin{eqnarray*}(4)&=&\lim_{N\to +\infty}\left[\left(-\gamma+\frac{\pi^2}{12}\right)H_{N-1}-\sum_{n=1}^{N-1}\frac{\frac{1}{2}H_n^{(2)}-H_n+\log(n+1)}{n}\right]\\&=&\frac{1}{2}\zeta(3)+\sum_{n\geq 1}\frac{H_n-\log(n+1)-\gamma}{n}\tag{5} \end{eqnarray*}$$

Now we may employ the asymptotic series for harmonic numbers in order to write $(5)$ in terms of Bernoulli numbers, values of the Riemann $\zeta$ function and the series

$$ \sum_{n\geq 1}\frac{\log(n+1)-\log(n)}{n}\stackrel{SBP}{=}\sum_{n\geq 1}\frac{\log(n+1)}{n(n+1)}=\int_{0}^{1}\frac{(1-x)\log(1-x)}{x\log x}\,dx \approx 1.25775 \tag{6}$$ that can be re-written in terms of Gregory coefficients or just as $\sum_{m\geq 1}\frac{(-1)^{m+1}\zeta(m+1)}{m}$.

^(Continues)

Answer 2

We have $H_x=\sum_{k=1}^\infty\frac1k-\frac1{x+k}$, thus, it follows from Cauchy products that we have

$$(H_x)^2=\sum_{k=0}^\infty\sum_{l=0}^k\left(\frac1{l+1}-\frac1{x+1+l}\right)\left(\frac1{k+1-l}-\frac1{x+1+k-l}\right)$$

Integrating term by term, we end up with

$$\int_0^1(H_x)^2\ dx=\sum_{k=0}^\infty\sum_{l=0}^k\left(\frac1{(l+1)(k+1-l)}+\frac{\ln\left(\frac{1+l}{2+l}\right)}{k+1-l}+\frac{\ln\left(\frac{1+k-l}{k-l}\right)}{l+1}+\frac{\ln\left(\frac{(1+l)(2+k-l)}{(2+l)(1+k-l)}\right)}{2l-k}\right)$$

Which, though not optimal, is more elementary than Jack D'Aurizio's answer.

Answer 3

$\newcommand{\bbx}[1]{\,\bbox[8px,border:1px groove navy]{\displaystyle{#1}}\,} \newcommand{\braces}[1]{\left\lbrace\,{#1}\,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\,{#1}\,\right\rbrack} \newcommand{\dd}{\mathrm{d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,\mathrm{e}^{#1}\,} \newcommand{\ic}{\mathrm{i}} \newcommand{\mc}[1]{\mathcal{#1}} \newcommand{\mrm}[1]{\mathrm{#1}} \newcommand{\pars}[1]{\left(\,{#1}\,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\root}[2][]{\,\sqrt[#1]{\,{#2}\,}\,} \newcommand{\totald}[3][]{\frac{\mathrm{d}^{#1} #2}{\mathrm{d} #3^{#1}}} \newcommand{\verts}[1]{\left\vert\,{#1}\,\right\vert}$ \begin{align} \int_{0}^{1}H_{x}^{2}\,\dd x & = \int_{0}^{1}\bracks{\Psi\pars{x + 1} + \gamma}^{\,2}\,\dd x = \gamma^{2} + \int_{0}^{1}\Psi^{\,2}\pars{x + 1}\,\dd x \\[5mm] & = \gamma^{2} + \lim_{q \to \infty}{1 \over q}\sum_{p = 1}^{q}\Psi^{\,2}\pars{{p \over q} + 1} = \gamma^{2} + \lim_{q \to \infty}{1 \over q}\sum_{p = 1}^{q - 1} \bracks{\Psi\pars{p \over q} + {q \over p}}^{2} \end{align}

$\ds{\Psi\pars{p \over q}}$ is evaluated with Gauss Digamma Theorem:

\begin{align} \Psi\pars{p \over q} & = -\gamma - \ln\pars{q} - {1 \over 2}\,\pi\cot\pars{\pi p \over q} + {1 \over 2}\sum_{k = 1}^{q - 1}\cos\pars{2\pi kp \over q} \ln\pars{2 - 2\cos\pars{2\pi k \over q}} \\[2mm] & p \in \mathbb{N}_{\ \geq\ 1}\,,\ q \in \mathbb{N}_{\ \geq\ 2}\,,\quad p < q \end{align}

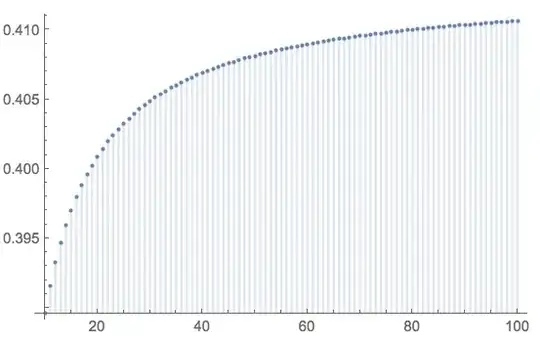
A 'numerical approximation' $\ds{\,\mc{N}_{q}}$ is given by:

\begin{align} \int_{0}^{1}H_{x}^{2}\,\dd x & \approx \gamma^{2} + {1 \over q}\sum_{p = 1}^{q - 1}\bracks{\Psi\pars{p \over q} + {q \over p}}^{2} \equiv \,\mc{N}_{q} \end{align} The figure shows $\ds{\,\mc{N}_{q}\ \mbox{vs.}\ q}$.