Calculating a distribution using fourier transform of the density

Question

I have an exercise where I got stuck and need some help.

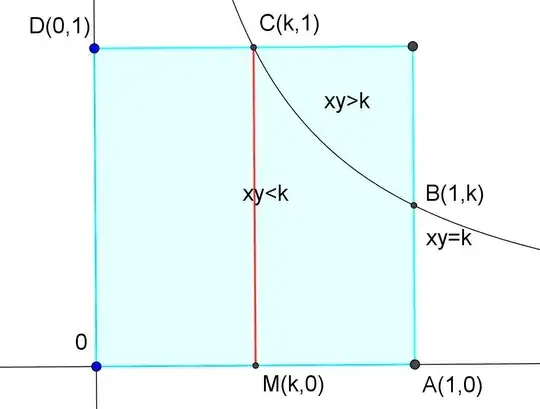
Let $X,Y$ be two i.i.d. random variables with $X,Y \sim U(0,1)$ and $T:=XY, Z:=YT$

-Calculate the distribution of $T$

Now following the hints I got, I did the following:

try to calculate $f_{XY}$ by considering an integrable function $g$ s.t. $$E(g(XY))=\int\int g(xy)f_X(x)f_Y(y)dxdy$$ then I did a change of variables to $u=x, v=xy$. This gives the determinant of the Jacobian to be $det(J)=\frac{1}{|u|}$, hence $$E(g(v))=\int\int g(v)f_X(u)f_Y(\frac{v}{u})\frac{1}{|u|}dudv$$ and $$f_{XY}(v)=\int f_X(u)f_Y(\frac{v}{u})\frac{1}{|u|}du$$ Now from the hints it is argued that if we chose $g(v)=e^{-ivk}$, we have the Fourier transform of the density in the expectation integral and by calculating the inverse we get the density distribution.

I have tried computing it, but I can't shake the feeling that I did an obvious mistake here...

So after I changed back the variables I got $$f_{XY}(xy)=\int e^{-ikxy}1_{0\leq x\leq 1}1_{0\leq y\leq 1}\frac{1}{|u|}dk$$ where $1_{A}$ is the indicator/characteristic function (due to $X,Y\sim U(0,1)$).

Whatever I try here, I get a complex valued function as the density which also results in a complex valued distribution which I suspect being wrong.

Can anyone help?

Answer 1

Here is a graphical way to obtain the cdf, then the pdf of RV $Z=XY$ when $X,Y$ are iid RV with $U(0,1)$ distribution.

$(X,Y)$ being a uniformly distributed point in the unit square $[0,1]^2$ (see figure below), the probability, for a fixed $k$, of event ''$XY<k$'' is (see remark below) the area of the corresponding region $OABCD$ delimited by line segments $OA,AB$, an arc of hyperbola $(H_k)$ with equation $y=\frac{k}{x}$ from $B$ to $C$, and line segments $CD$ and $DO$.

This area is easily computable by splitting it into

• the area of a rectangle (with value $1 \times k$) and

• the area below the arc of curve $(H_k)$, with value $\int_k^1 \dfrac{k}{x}dx=k [\ln(x)]_k^1=-k \ln k$ (don't forget that $0<k<1$ implies $\ln k < 0$).

Gathering these two values, we obtain the following expression for the cdf of $Z$:

$$F_Z(k):=P(Z<k)=P(XY<k)=k - k \ln k$$

with derivative, its pdf:

$$f_Z(k)=1-k\dfrac{1}{k}-\ln k= -\ln k.$$

Easy, isn't it ?

Remark: A little elementary step has been skipped: strictly speaking, we should have said that this probability is the ratio of the area OABCD to the total area, with a total area equal to $1$...