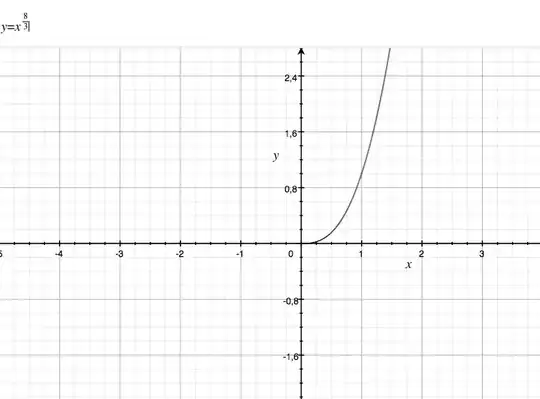
One of the problems here is that you assumed $\left(-x\right)^\frac 8 3=\left(-x^\frac 1 3\right)^8$, when it equals $\left(\left(-x\right)^\frac 1 3\right)^8$. This has multiple solutions. For positive non-zero $x$,
$$\left(-x\right)^\frac 8 3 = x^\frac 8 3\left(\left(-1\right)^\frac 1 3\right)^8$$
Where $\left(-1\right)^\frac 1 3$ has 3 solutions:
$$-1\\\\0.5+\frac{i\sqrt3}2\\\\0.5-\frac{i\sqrt3}2\\\\$$
If you define $n^\frac 1 3$ as the real root, then $\left(-x\right)^\frac 8 3 = x^\frac 8 3\left(-1\right)^8=x^\frac 8 3$, which is defined over all of $\mathbb R$.
If you define $n^\frac 1 3$ as the principal root,
$$\begin{align}
\left(-x\right)^\frac 8 3
&= x^\frac 8 3\left(0.5+\frac{i\sqrt3}2\right)^8
\\&=x^\frac 8 3\left(-0.5+\frac{i\sqrt3}2\right)
\\&=-0.5x^\frac 8 3+\frac{ix^\frac 8 3\sqrt 3}2
\end{align}$$
which is a complex number, and the principal root is usually taken.