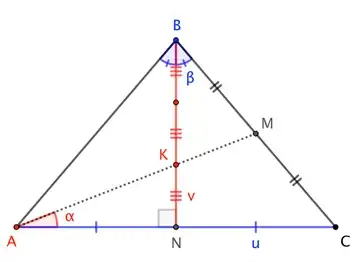
Given an isosceles $\triangle ABC$, where $\overline{AB} \cong \overline{BC}$, let $M$ be the midpoint of $\overline{BC}$. The angle between $\overline{AC}$ and median $\overline{AM}$ is $\alpha$. How can I find the angles of the triangle?
-
You need 3 quantities to determine a triangle. We appear to only have 2 ... $AB=BC$ and $\alpha$ ... is there something you are not telling us ? – Donald Splutterwit Mar 11 '17 at 22:16
-
@DonaldSplutterwit You need three quantities to determine a triangle. But, I think that the angles could be figured with the two quantities. Did you note that $AM$ is the median? – frederick99 Mar 11 '17 at 22:19
-
That's all I think. The problem is from a contest which took part yesterday – student28 Mar 11 '17 at 22:19
-
@frederick99 You are right ... the implicit third piece of info is that the angles of a triangle add upto $180$ ... – Donald Splutterwit Mar 11 '17 at 22:44
-
It is implied anyways. To determine a triangle fully, you need another three quantities. :) – frederick99 Mar 11 '17 at 22:48
-
Why don't you validate answers that ... answer your question ? – Jean Marie Dec 30 '17 at 06:31
-
@student28: I appreciate the checkmark. However, given that JeanMarie's solution is a vast improvement on mine, I recommend accepting that one instead. – Blue Feb 03 '18 at 06:18
2 Answers
Inspired by your solution, @Blue, and along the same lines, taking the same notations (with $K$ center of gravity at the intersection of median $AM$ and altitude-median $BN$ with $BN=3KN$), I propose a shorter solution that does not use point $P$. Here it is:
Let $u=AN=NC$. We have, by definition of a tangent:
$\tan \alpha=\dfrac{KN}{u},$
$\tan \beta=\dfrac{u}{BN}=\dfrac{u}{3KN},$
Therefore: $ \ \ \tan \alpha \tan \beta=\dfrac{1}{3} \ \ \ \implies \ \ \ \ \beta=\displaystyle\arctan\left(\dfrac{1}{3 \tan \alpha}\right).$
Remark: I have erased my so complicated previous proof.
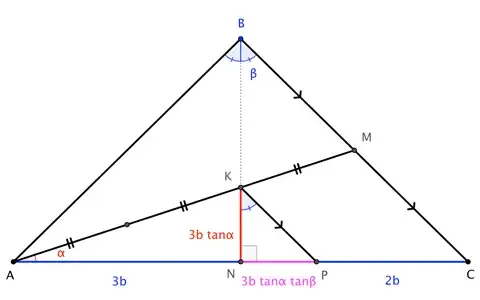
Edit by @Blue. This refinement is so good that I had to draw a picture!
$$\tan \alpha \tan\beta = \frac{v}{u}\cdot\frac{u}{3v} = \frac{1}{3}$$
Also, I recommend that OP accept this answer.
- 75,673
- 81,803
To avoid fractions, take $\angle B = 2\beta$ and $|\overline{AC}| = 6b$. We may consider the problem solved once we have expressed $\beta$ in terms of $\alpha$.
Let the perpendicular from $B$ meet $\overline{AC}$ and $\overline{AM}$ at at $N$ and $K$, respectively. Take $P$ on $\overline{AC}$ such that $\overline{KP} \parallel \overline{BC}$.
Since $K$, as the intersection of two medians, is the centroid of $\triangle ABC$, we "know" that $|\overline{KM}|:|\overline{AM}| = 1:3$. The parallel $\overline{KP}$ carries this ratio over so that $|\overline{PC}|:|\overline{AC}| = 1:3$. That is, $|\overline{PC}| = 2b$, and we have $$|\overline{NP}| = 1b \tag{1}$$
Moreover, $$|\overline{AN}| = 3 b \quad \to \quad |\overline{KN}| = 3b \tan\alpha \quad\to\quad |\overline{NP}| = 3 b\tan\alpha \tan \beta \tag{2}$$
Therefore, $$3b\tan\alpha\tan\beta = 1b\quad\to\quad\tan\alpha\tan\beta = \frac{1}{3} \quad\to\quad \beta = \operatorname{atan}\left(\frac{1}{3}\cot\alpha\right)\tag{3}$$ $\square$
- 75,673
-
Materializing quantity $3b\tan\alpha\tan\beta$ is a good idea. Besides, I have much appreciated your elegance in recommending my solution. – Jean Marie Feb 04 '18 at 06:15
-
1@JeanMarie: I'm just trying to deflect attention from the embarrassment of focussing on the trisection of the wrong median. ;) But seriously, yours is clearly the better solution, and deserves to be "accepted" over mine. (I'm happy enough to take some credit for "inspiring" it!) – Blue Feb 04 '18 at 07:19
-
As you are interested by classical geometry, have you noticed my recent question about inversion transform (https://math.stackexchange.com/q/2626356) ? – Jean Marie Feb 04 '18 at 07:35
-
@JeanMarie: I've seen the question, but I can't think of anything to contribute ... yet. – Blue Feb 04 '18 at 07:44